4 GLM - Logistic: Example, BPD

example walk through:

https://stats.idre.ucla.edu/r/dae/logit-regression/

info:

https://onlinecourses.science.psu.edu/stat504/node/216/

sjPlot::tab_model (HTML only)

http://www.strengejacke.de/sjPlot/articles/sjtlm.html#changing-summary-style-and-content

finafit

https://www.r-bloggers.com/elegant-regression-results-tables-and-plots-in-r-the-finalfit-package/

library(tidyverse)
library(haven)        # read in SPSS dataset
library(furniture)    # nice table1() descriptives
library(stargazer)    # display nice tables: summary & regression
library(texreg)       # Convert Regression Output to LaTeX or HTML Tables
library(psych)        # contains some useful functions, like headTail
library(car)          # Companion to Applied Regression
library(pscl)         # psudo R-squared function

4.1 Background

Simple example demonstrating basic modeling approach: Data on Bronchopulmonary Dysplasia (BPD) from 223 low birth weight infants (weighing less than 1750 grams).

4.1.1 Source

Data courtesy of Dr. Linda Van Marter.

4.1.2 Reference

Van Marter, L.J., Leviton, A., Kuban, K.C.K., Pagano, M. & Allred, E.N. (1990). Maternal glucocorticoid therapy and reduced risk of bronchopulmonary dysplasia. Pediatrics, 86, 331-336.

The data are from a study of low birth weight infants in a neonatal intensive care unit. The study was designed to examine the development of bronchopulmonary dysplasia (BPD), a chronic lung disease, in a sample of 223 infants weighing less than 1750 grams. The response variable is binary, denoting whether an infant develops BPD by day 28 of life (where BPD is defined by both oxygen requirement and compatible chest radiograph).

4.1.3 Variables

  • bpd(0 [N],1 [Y])
  • brthwght (grams)
  • gestage (weeks)
  • toxemia (0 [N] ,1 [Y]) in mother
bpd_raw <- read.table("https://raw.githubusercontent.com/CEHS-research/eBook_regression/master/data/VanMarter_%20BPD.txt?token=AScXBcwRurGPiBMhNmlD3RyY9VU1Bh7lks5bz50qwA%3D%3D", 
                      header      = TRUE, 
                      strip.white = TRUE)
n <- nrow(bpd_raw)
n
[1] 223
str(bpd_raw)
'data.frame':   223 obs. of  4 variables:
 $ bpd     : int  1 0 1 0 0 0 1 0 1 1 ...
 $ brthwght: int  850 1500 1360 960 1560 1120 810 1620 1000 700 ...
 $ gestage : int  27 33 32 35 33 29 28 32 30 26 ...
 $ toxemia : int  0 0 0 1 0 0 0 0 0 0 ...
head(bpd_raw)
# A tibble: 6 x 4
    bpd brthwght gestage toxemia
* <int>    <int>   <int>   <int>
1     1      850      27       0
2     0     1500      33       0
3     1     1360      32       0
4     0      960      35       1
5     0     1560      33       0
6     0     1120      29       0
bpd_clean <- bpd_raw %>% 
  dplyr::mutate(toxemia = factor(toxemia,
                                 levels = c(0, 1),
                                 labels = c("No", "Yes")))
summary(bpd_clean)
      bpd            brthwght       gestage      toxemia  
 Min.   :0.0000   Min.   : 450   Min.   :25.00   No :194  
 1st Qu.:0.0000   1st Qu.: 895   1st Qu.:28.00   Yes: 29  
 Median :0.0000   Median :1140   Median :30.00            
 Mean   :0.3408   Mean   :1173   Mean   :30.09            
 3rd Qu.:1.0000   3rd Qu.:1465   3rd Qu.:32.00            
 Max.   :1.0000   Max.   :1730   Max.   :37.00

4.2 Logistic Regresion

4.2.1 Fit the Models

fit_glm_0 <- glm(bpd ~ 1, 
                 data = bpd_clean, 
                 family = binomial(link = "logit")) 


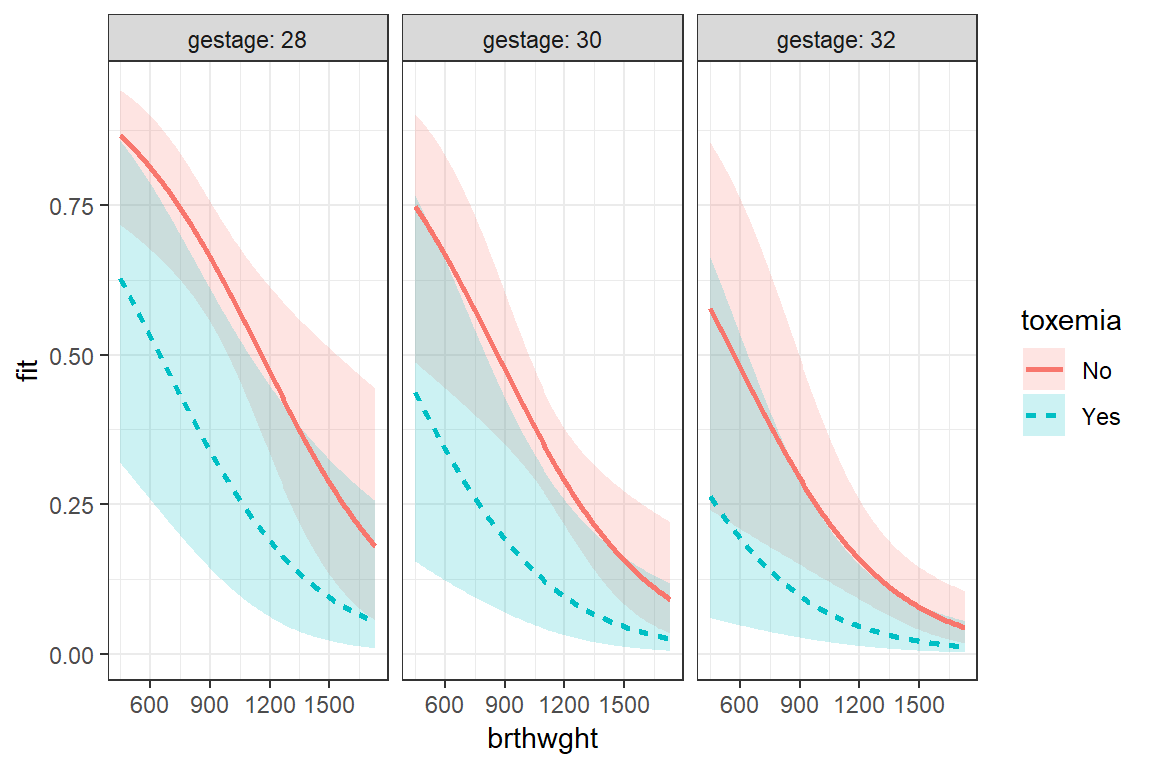
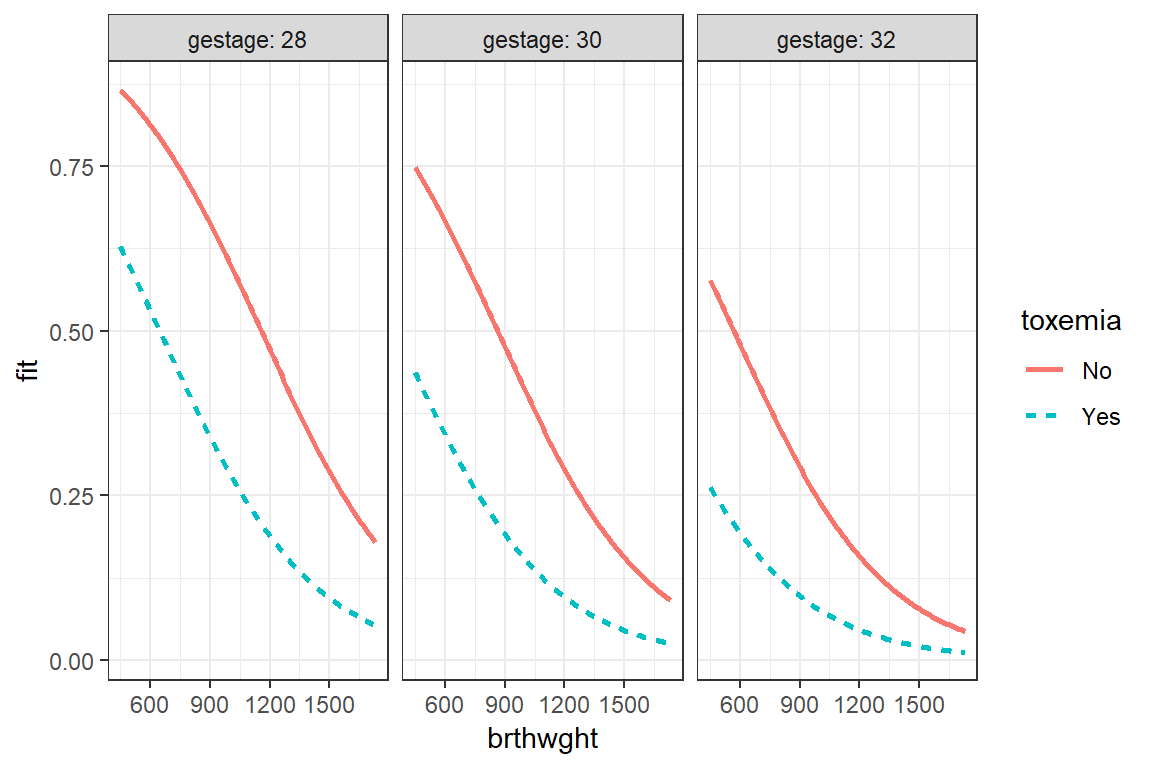
fit_glm_1 <- glm(bpd ~ I(brthwght/100) + gestage + toxemia, 
                 data = bpd_clean, 
                 family = binomial(link = "logit"))

4.2.1.1 Log Likelihood

logLik(fit_glm_0)
'log Lik.' -143.07 (df=1)
logLik(fit_glm_1)
'log Lik.' -101.8538 (df=4)

4.2.1.2 Deviance

deviance(fit_glm_0)
[1] 286.14
deviance(fit_glm_1)
[1] 203.7075

4.2.2 GoF Measures

4.2.2.1 AIC

AIC(fit_glm_0)
[1] 288.14
AIC(fit_glm_1)
[1] 211.7075

4.2.2.2 Logistic R^2

http://thestatsgeek.com/2014/02/08/r-squared-in-logistic-regression/

Technically, \(R^2\) cannot be computed the same way in logistic regression as it is in OLS regression. The \(pseudo-R^2\), in logistic regression, is defined as \(1−\frac{L_1}{L_0}\), where \(L_0\) represents the log likelihood for the “constant-only” or NULL model and \(L_1\) is the log likelihood for the full model with constant and predictors.

4.2.2.3 McFadden’s pseud- R^2

\[ R^2_{McF} = 1 - \frac{L_1}{L_0} \]

MFR2 <- 1 - (logLik(fit_glm_1)/logLik(fit_glm_0))
MFR2
'log Lik.' 0.2880843 (df=4)

4.2.2.4 Cox & Snell

\(l = e^{L}\), sinc \(L\) is the log of the likelihood and \(l\) is the likelihood…\(log(l) = L\)

\[ R^2_{CS} = 1 - \Bigg( \frac{l_0}{l_1} \Bigg) ^{2 \backslash n} \\ n = \text{sample size} \]

CSR2 <- 1 - (exp(logLik(fit_glm_0))/exp(logLik(fit_glm_1)))^(2/n)
CSR2
'log Lik.' 0.3090253 (df=1)

4.2.2.5 Nagelkerke or Cragg and Uhler’s

\[ R^2_{Nag} = \frac{1 - \Bigg( \frac{l_0}{l_1} \Bigg) ^{2 \backslash n}} {1 - \Big( l_0 \Big) ^{2 \backslash n}} \]

NR2 <- CSR2 / (1 - exp(logLik(fit_glm_0))^(2/n))
NR2 
'log Lik.' 0.4275191 (df=1)

4.2.2.6 Several with the pscl::pR2() function

pscl::pR2(fit_glm_1)
         llh      llhNull           G2     McFadden         r2ML 
-101.8537711 -143.0699809   82.4324196    0.2880843    0.3090253 
        r2CU 
   0.4275191

4.2.3 Parameter Estimates

4.2.3.1 Logit Scale

fit_glm_1 %>% coef()
    (Intercept) I(brthwght/100)         gestage      toxemiaYes 
     13.9360826      -0.2643578      -0.3885357      -1.3437865

4.2.3.2 Odds Ratio Scale

fit_glm_1 %>% coef() %>% exp()
    (Intercept) I(brthwght/100)         gestage      toxemiaYes 
   1.128142e+06    7.676988e-01    6.780490e-01    2.608561e-01

4.2.3.3 Confidence Intervals - OR sclae

fit_glm_1 %>% confint() %>% exp()
                       2.5 %       97.5 %
(Intercept)     4.402379e+03 5.591330e+08
I(brthwght/100) 6.511832e-01 8.967757e-01
gestage         5.351280e-01 8.414808e-01
toxemiaYes      7.314875e-02 8.078916e-01

4.2.4 Significance of Terms

4.2.4.1 Likelihood Ratio Test of all Nested Models

anova(fit_glm_0, fit_glm_1)
# A tibble: 2 x 4
  `Resid. Df` `Resid. Dev`    Df Deviance
*       <dbl>        <dbl> <dbl>    <dbl>
1         222         286.    NA     NA  
2         219         204.     3     82.4

4.2.4.2 Sequential LRTs: for adding one variable at a time

anova(fit_glm_1, test = "Chisq")
# A tibble: 4 x 5
     Df Deviance `Resid. Df` `Resid. Dev` `Pr(>Chi)`
* <int>    <dbl>       <int>        <dbl>      <dbl>
1    NA    NA            222         286.  NA       
2     1    62.4          221         224.   2.78e-15
3     1    14.5          220         209.   1.41e- 4
4     1     5.52         219         204.   1.88e- 2

4.2.5 Parameter Estimates

4.2.5.1 Raw Output

summary(fit_glm_1) 

Call:
glm(formula = bpd ~ I(brthwght/100) + gestage + toxemia, family = binomial(link = "logit"), 
    data = bpd_clean)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.8400  -0.7029  -0.3352   0.7261   2.9902  

Coefficients:
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)     13.93608    2.98255   4.673 2.98e-06 ***
I(brthwght/100) -0.26436    0.08123  -3.254  0.00114 ** 
gestage         -0.38854    0.11489  -3.382  0.00072 ***
toxemiaYes      -1.34379    0.60750  -2.212  0.02697 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 286.14  on 222  degrees of freedom
Residual deviance: 203.71  on 219  degrees of freedom
AIC: 211.71

Number of Fisher Scoring iterations: 5

4.2.5.2 sjPlot - HTML tables

JUST HTML for now…

Parameters Exponentiated:

sjPlot::tab_model(fit_glm_1)
  bpd
Predictors Odds Ratios CI p
(Intercept) 1128141.99 4402.38 – 559132968.51 <0.001
I(brthwght/100) 0.77 0.65 – 0.90 0.001
gestage 0.68 0.54 – 0.84 0.001
toxemiaYes 0.26 0.07 – 0.81 0.027
Observations 223
Cox & Snell’s R2 / Nagelkerke’s R2 0.309 / 0.428 
sjPlot::tab_model(fit_glm_1,
                  emph.p = TRUE,
                  pred.labels = c("(Intercept)",
                                  "Birthweight, 100 grams",
                                  "Gestational Age, week",
                                  "Mother had Toxemia"))
  bpd
Predictors Odds Ratios CI p
(Intercept) 1128141.99 4402.38 – 559132968.51 <0.001
Birthweight, 100 grams 0.77 0.65 – 0.90 0.001
Gestational Age, week 0.68 0.54 – 0.84 0.001
Mother had Toxemia 0.26 0.07 – 0.81 0.027
Observations 223
Cox & Snell’s R2 / Nagelkerke’s R2 0.309 / 0.428

4.2.5.3 texreg default

texreg::screenreg(fit_glm_1)

============================
                 Model 1    
----------------------------
(Intercept)        13.94 ***
                   (2.98)   
I(brthwght/100)    -0.26 ** 
                   (0.08)   
gestage            -0.39 ***
                   (0.11)   
toxemiaYes         -1.34 *  
                   (0.61)   
----------------------------
AIC               211.71    
BIC               225.34    
Log Likelihood   -101.85    
Deviance          203.71    
Num. obs.         223       
============================
*** p < 0.001, ** p < 0.01, * p < 0.05

4.2.5.4 texreg Confidence Intervals on Logit Scale

texreg::screenreg(fit_glm_1,
                  ci.force = TRUE)

===============================
                 Model 1       
-------------------------------
(Intercept)        13.94 *     
                 [ 8.09; 19.78]
I(brthwght/100)    -0.26 *     
                 [-0.42; -0.11]
gestage            -0.39 *     
                 [-0.61; -0.16]
toxemiaYes         -1.34 *     
                 [-2.53; -0.15]
-------------------------------
AIC               211.71       
BIC               225.34       
Log Likelihood   -101.85       
Deviance          203.71       
Num. obs.         223          
===============================
* 0 outside the confidence interval

4.2.5.5 texreg exponentiate the betas (SE are not exp)

texreg::screenreg(fit_glm_1,
                  override.coef = list(fit_glm_1 %>% coef() %>% exp()))

===============================
                 Model 1       
-------------------------------
(Intercept)      1128141.99 ***
                      (2.98)   
I(brthwght/100)        0.77 ** 
                      (0.08)   
gestage                0.68 ***
                      (0.11)   
toxemiaYes             0.26 *  
                      (0.61)   
-------------------------------
AIC                  211.71    
BIC                  225.34    
Log Likelihood      -101.85    
Deviance             203.71    
Num. obs.            223       
===============================
*** p < 0.001, ** p < 0.01, * p < 0.05

4.2.6 Marginal Model Plot

4.2.6.1 Manually Specified

summary(bpd_clean)
      bpd            brthwght       gestage      toxemia  
 Min.   :0.0000   Min.   : 450   Min.   :25.00   No :194  
 1st Qu.:0.0000   1st Qu.: 895   1st Qu.:28.00   Yes: 29  
 Median :0.0000   Median :1140   Median :30.00            
 Mean   :0.3408   Mean   :1173   Mean   :30.09            
 3rd Qu.:1.0000   3rd Qu.:1465   3rd Qu.:32.00            
 Max.   :1.0000   Max.   :1730   Max.   :37.00            
effects::Effect(focal.predictors = c("brthwght", "toxemia", "gestage"),
                mod = fit_glm_1,
                xlevels = list(brthwght = seq(from = 450, to = 1730, by = 10),
                               gestage = c(28, 30, 32))) %>% 
  data.frame() %>% 
  dplyr::mutate(gestage = factor(gestage)) %>% 
  ggplot(aes(x = brthwght,
             y = fit)) +
  geom_ribbon(aes(ymin = lower,
                  ymax = upper,
                  fill = toxemia),
              alpha = .2) +
  geom_line(aes(linetype = toxemia,
                color = toxemia),
            size = 1) +
  facet_grid(. ~ gestage, labeller = label_both) +
  theme_bw()

effects::Effect(focal.predictors = c("brthwght", "toxemia", "gestage"),
                mod = fit_glm_1,
                xlevels = list(brthwght = seq(from = 450, to = 1730, by = 10),
                               gestage = c(28, 30, 32))) %>% 
  data.frame() %>% 
  dplyr::mutate(gestage = factor(gestage)) %>% 
  ggplot(aes(x = brthwght,
             y = fit)) +
  geom_line(aes(linetype = toxemia,
                color = toxemia),
            size = 1) +
  facet_grid(. ~ gestage, labeller = label_both) +
  theme_bw()

4.2.7 Residual Diagnostics

4.2.7.1 sjPlot

sjPlot::plot_model(fit_glm_1, type = "diag")
NULL

4.2.7.2 base R graphics

plot(fit_glm_1)