10 Logistic Regression - Ex: Depression (Hoffman)

library(tidyverse)
library(haven)        # read in SPSS dataset
library(furniture)    # nice table1() descriptives
library(stargazer)    # display nice tables: summary & regression
library(texreg)       # Convert Regression Output to LaTeX or HTML Tables
library(texreghelpr)  # GITHUB: sarbearschartz/texreghelpr
library(psych)        # contains some useful functions, like headTail
library(car)          # Companion to Applied Regression
library(sjPlot)       # Quick plots and tables for models
library(pscl)         # psudo R-squared function
library(glue)         # Interpreted String Literals 
library(interactions) # interaction plots
library(sjPlot)       # various plots
library(performance)  # r-squared values

This dataset comes from John Hoffman’s textbook: Regression Models for Categorical, Count, and Related Variables: An Applied Approach (2004) Amazon link, 2014 edition

Chapter 3: Logistic and Probit Regression Models

Dataset: The following example uses the SPSS data set Depress.sav. The dependent variable of interest is a measure of life satisfaction, labeled satlife.

df_depress <- haven::read_spss("https://raw.githubusercontent.com/CEHS-research/data/master/Hoffmann_datasets/depress.sav") %>% 
  haven::as_factor()

tibble::glimpse(df_depress)

Rows: 118
Columns: 14
$ id      <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ...
$ age     <dbl> 39, 41, 42, 30, 35, 44, 31, 39, 35, 33, 38, 31, 40, 44, 43,...
$ iq      <dbl> 94, 89, 83, 99, 94, 90, 94, 87, NA, 92, 92, 94, 91, 86, 90,...
$ anxiety <fct> medium low, medium low, medium high, medium low, medium low...
$ depress <fct> medium, medium, high, medium, low, low, medium, medium, med...
$ sleep   <fct> low, low, low, low, high, low, NA, low, low, low, high, low...
$ sex     <fct> female, female, female, female, female, male, female, femal...
$ lifesat <fct> low, low, low, low, high, high, low, high, low, low, high, ...
$ weight  <dbl> 4.9, 2.2, 4.0, -2.6, -0.3, 0.9, -1.5, 3.5, -1.2, 0.8, -1.9,...
$ satlife <dbl> 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1,...
$ male    <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0,...
$ sleep1  <dbl> 0, 0, 0, 0, 1, 0, NA, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0...
$ newiq   <dbl> 2.21, -2.79, -8.79, 7.21, 2.21, -1.79, 2.21, -4.79, NA, 0.2...
$ newage  <dbl> 1.5424, 3.5424, 4.5424, -7.4576, -2.4576, 6.5424, -6.4576, ...

psych::headTail(df_depress)

# A tibble: 9 x 14
  id    age   iq    anxiety depress sleep sex   lifesat weight satlife male 
  <chr> <chr> <chr> <fct>   <fct>   <fct> <fct> <fct>   <chr>  <chr>   <chr>
1 1     39    94    medium~ medium  low   fema~ low     4.9    0       0    
2 2     41    89    medium~ medium  low   fema~ low     2.2    0       0    
3 3     42    83    medium~ high    low   fema~ low     4      0       0    
4 4     30    99    medium~ medium  low   fema~ low     -2.6   0       0    
5 ...   ...   ...   <NA>    <NA>    <NA>  <NA>  <NA>    ...    ...     ...  
6 115   39    87    medium~ medium  low   male  low     <NA>   0       1    
7 116   41    86    medium~ medium  high  male  low     -1     0       1    
8 117   33    89    low     low     high  male  high    6.5    1       1    
9 118   42    <NA>  medium~ medium  low   fema~ low     4.9    0       0    
# ... with 3 more variables: sleep1 <chr>, newiq <chr>, newage <chr>

df_depress %>% 
  dplyr::select(satlife, lifesat) %>% 
  table() %>% 
  addmargins()

       lifesat
satlife high low Sum
    0      0  65  65
    1     52   0  52
    Sum   52  65 117

10.1 Exploratory Data Analysis

Dependent Variable = satlife (numeric version) or lifesat (factor version)

10.1.1 Visualize

df_depress %>% 
  ggplot(aes(x = age,
             y = satlife)) +
  geom_count() +
  geom_smooth(method = "lm") +
  theme_bw() +
  labs(x = "Age in Years",
       y = "Life Satisfaction, numeric")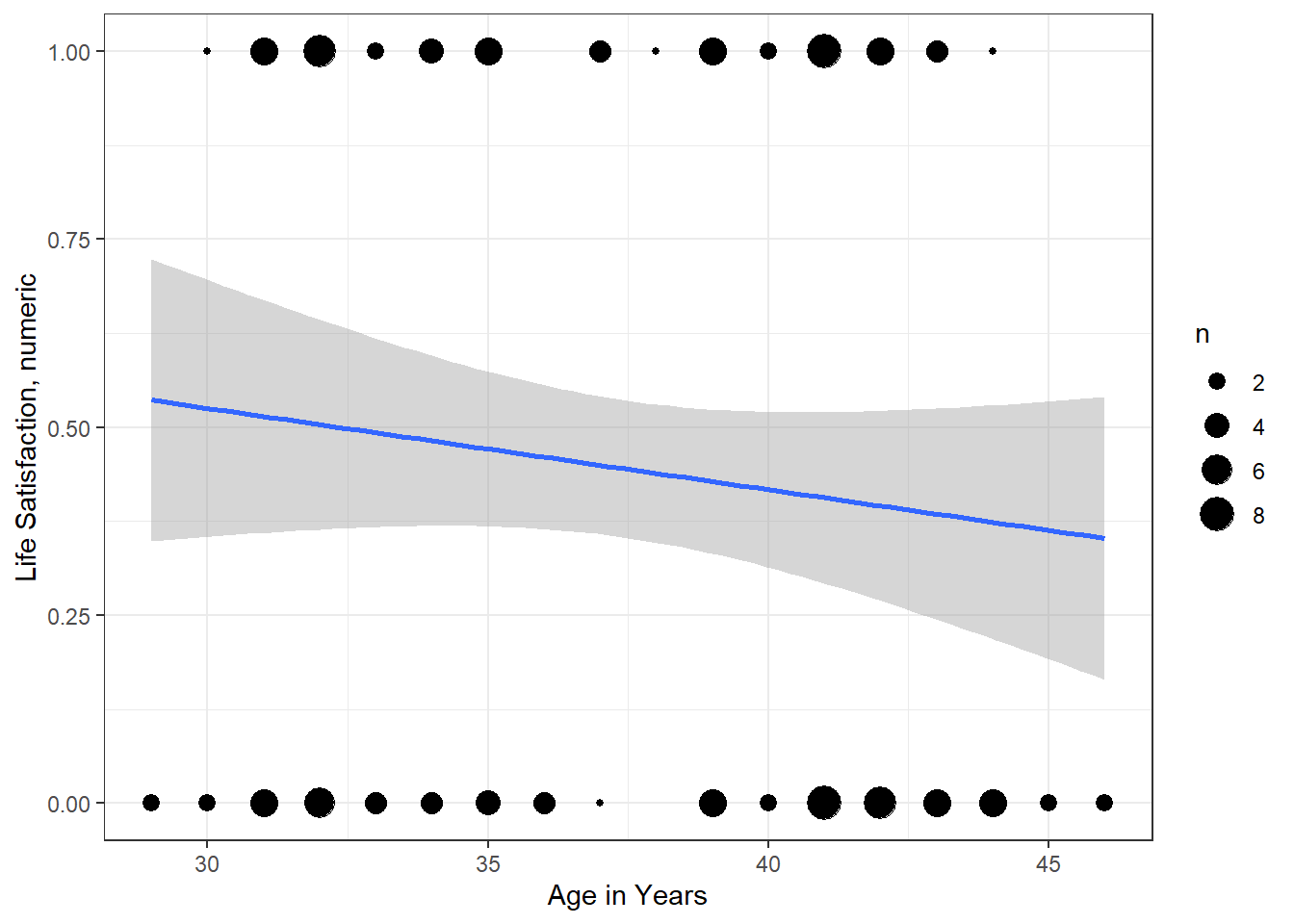

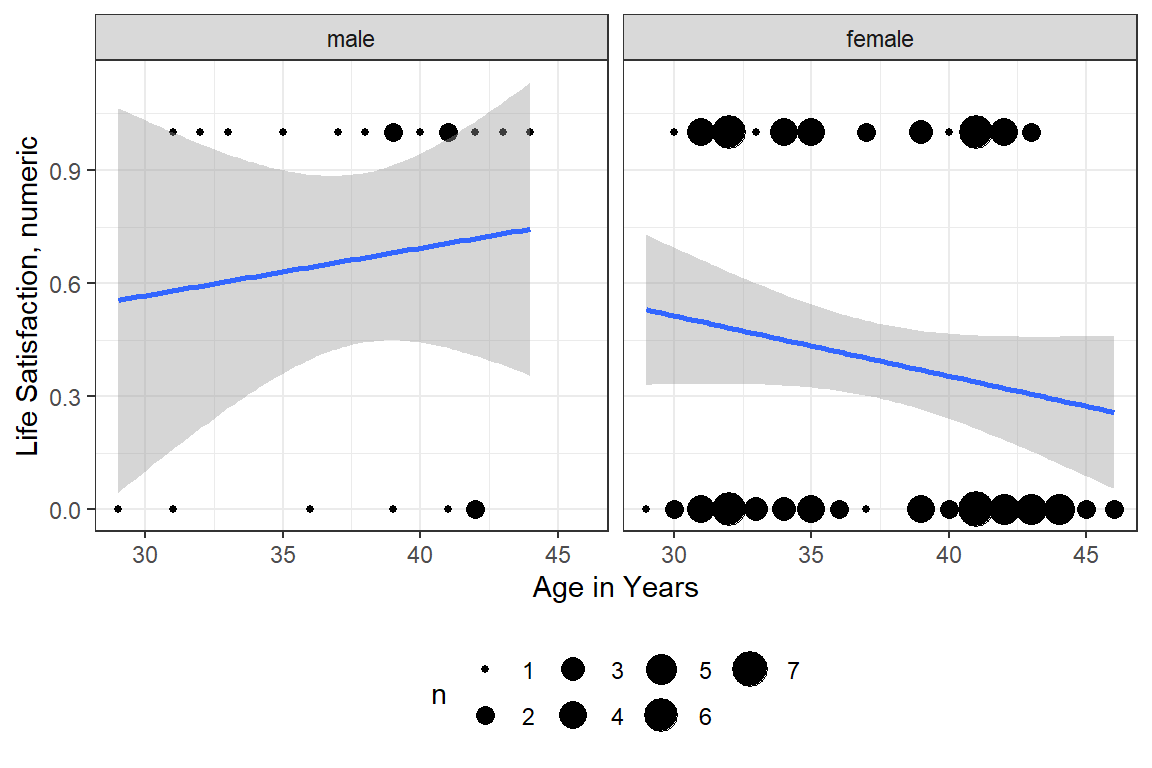
Figure 10.1: Hoffman’s Figure 2.3, top of page 46

df_depress %>% 
  ggplot(aes(x = age,
             y = satlife)) +
  geom_count() +
  geom_smooth(method = "lm") +
  theme_bw() +
  labs(x = "Age in Years",
       y = "Life Satisfaction, numeric") +
  facet_grid(~ sex) +
  theme(legend.position = "bottom")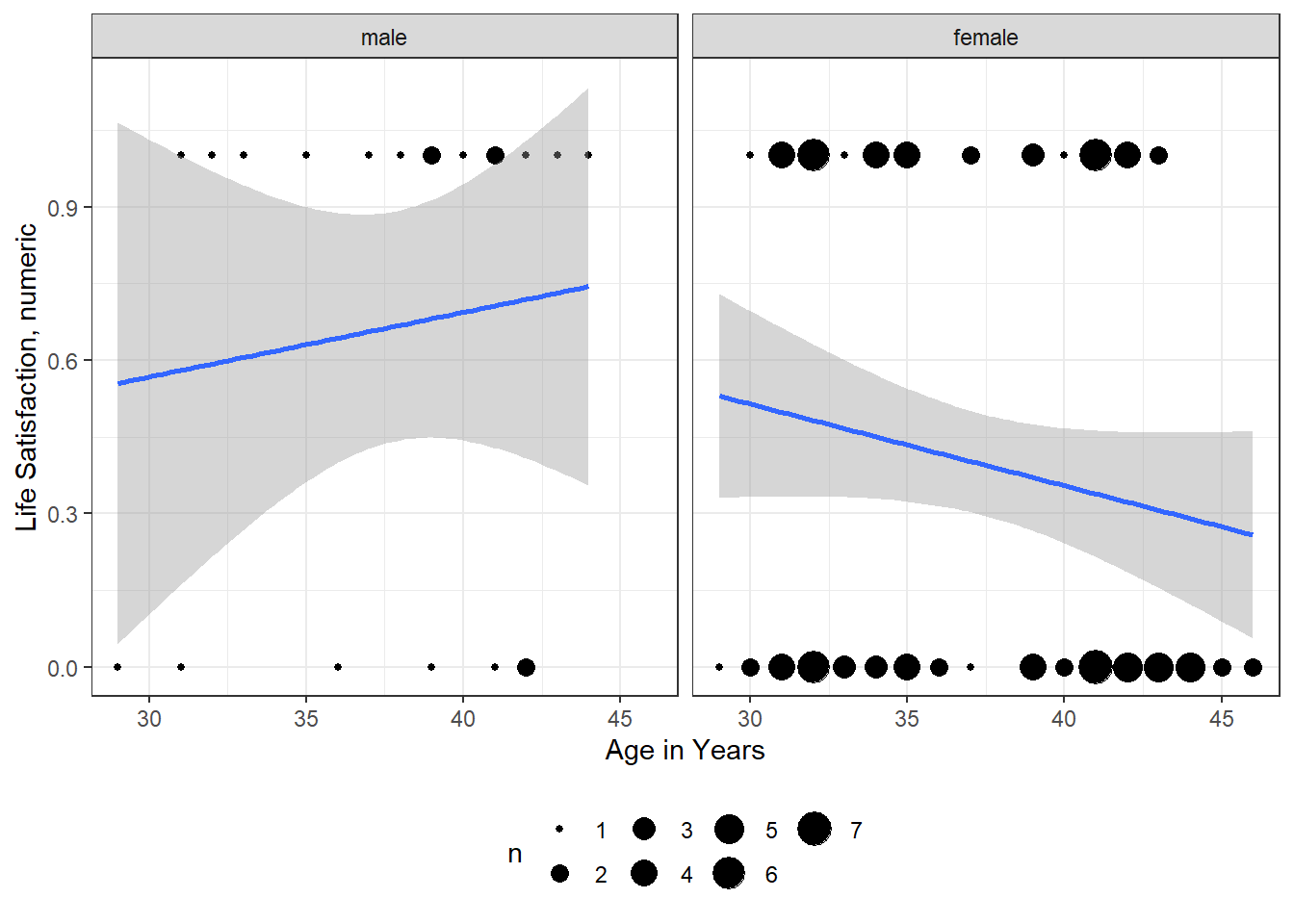

10.1.2 Summary Table

Independent = sex

df_depress %>% 
  dplyr::select(lifesat, sex) %>% 
  table() %>% 
  addmargins()

       sex
lifesat male female Sum
   high   14     38  52
   low     7     58  65
   Sum    21     96 117

df_depress %>% 
  dplyr::group_by(sex) %>% 
  furniture::table1(lifesat,
                    total = TRUE,
                    caption = "Hoffman's EXAMPLE 3.1 Cross-Tabulation of Gender and Life Satisfaction (top page 50)",
                    output = "markdown")

Table 10.1: Hoffman’s EXAMPLE 3.1 Cross-Tabulation of Gender and Life Satisfaction (top page 50)
	Total	male	female
	n = 117	n = 21	n = 96
lifesat
high	52 (44.4%)	14 (66.7%)	38 (39.6%)
low	65 (55.6%)	7 (33.3%)	58 (60.4%)

10.2 Calcualte: Probability, Odds, and Odds-Ratios

10.2.1 Marginal, over all the sample

Tally the number of participants happy and not happy (i.e. depressed).

df_depress %>% 
  dplyr::select(satlife) %>% 
  table() %>% 
  addmargins()

.
  0   1 Sum 
 65  52 117

10.2.1.1 Probability of being happy

\[ prob_{yes} = \frac{n_{yes}}{n_{total}} = \frac{n_{yes}}{n_{yes} + n_{no}} \]

prob <- 52 / 117

prob

[1] 0.4444444

10.2.1.2 Odds of being happy

\[ odds_{yes} = \frac{n_{yes}}{n_{no}} = \frac{n_{yes}}{n_{total} - n_{yes}} \]

odds <- 52/65

odds

[1] 0.8

\[ odds_{yes} = \frac{prob_{yes}}{prob_{no}} = \frac{prob_{yes}}{1 - prob_{yes}} \]

prob/(1 - prob)

[1] 0.8

10.2.2 Comparing by Sex

Cross-tabulate happiness (satlife) with sex (male vs. female).

df_depress %>% 
  dplyr::select(satlife, sex) %>% 
  table() %>% 
  addmargins()

       sex
satlife male female Sum
    0      7     58  65
    1     14     38  52
    Sum   21     96 117

10.2.2.1 Probability of being happy, by sex

Reference category = male

prob_male <- 14 / 21

prob_male

[1] 0.6666667

Comparison Category = female

prob_female <- 38 / 96

prob_female

[1] 0.3958333

10.2.2.2 Odds of being happy, by sex

Reference category = male

odds_male <- 14 / 7

odds_male

[1] 2

Comparison Category = female

odds_female <- 38 / 58


odds_female

[1] 0.6551724

10.2.2.3 Odds-Ratio for sex

\[ OR_{\text{female vs. male}} = \frac{odds_{female}}{odds_{male}} \]

odds_ratio <- odds_female / odds_male

odds_ratio

[1] 0.3275862

\[ OR_{\text{female vs. male}} = \frac{\frac{prob_{female}}{1 - prob_{female}}}{\frac{prob_{male}}{1 - prob_{male}}} \]

(prob_female / (1 - prob_female)) / (prob_male / (1 - prob_male))

[1] 0.3275862

\[ OR_{\text{female vs. male}} = \frac{\frac{n_{yes|female}}{n_{no|female}}}{\frac{n_{yes|male}}{n_{no|male}}} \]

((38 / 58)/(14 / 7))

[1] 0.3275862

10.3 Logisitc Regression Model 1: one IV

10.3.1 Fit the Unadjusted Model

fit_glm_1 <- glm(satlife ~ sex,
                 data = df_depress,
                 family = binomial(link = "logit"))

fit_glm_1 %>% summary() %>% coef()

              Estimate Std. Error   z value   Pr(>|z|)
(Intercept)  0.6931472  0.4629100  1.497369 0.13429719
sexfemale   -1.1160040  0.5077822 -2.197800 0.02796333

summary(fit_glm_1)


Call:
glm(formula = satlife ~ sex, family = binomial(link = "logit"), 
    data = df_depress)

Deviance Residuals: 
   Min      1Q  Median      3Q     Max  
-1.482  -1.004  -1.004   1.361   1.361  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)   0.6931     0.4629   1.497    0.134  
sexfemale    -1.1160     0.5078  -2.198    0.028 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 160.75  on 116  degrees of freedom
Residual deviance: 155.62  on 115  degrees of freedom
  (1 observation deleted due to missingness)
AIC: 159.62

Number of Fisher Scoring iterations: 4

10.3.2 Tabulate Parameters

10.3.2.1 Logit Scale

texreg::knitreg(fit_glm_1,
                caption = "Hoffman's EXAMPLE 3.2 A Loistic Regression Model of Gender and Life Satisfaction, top of page 51",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4)

Hoffman’s EXAMPLE 3.2 A Loistic Regression Model of Gender and Life Satisfaction, top of page 51
	Model 1
(Intercept)	0.6931 (0.4629)
sexfemale	-1.1160 (0.5078)^*
AIC	159.6205
BIC	165.1449
Log Likelihood	-77.8103
Deviance	155.6205
Num. obs.	117
p < 0.001; p < 0.01; p < 0.05

10.3.2.2 Both Logit and Odds-ratio Scales

texreg::knitreg(list(fit_glm_1,
                     texreghelpr::extract_glm_exp(fit_glm_1)),
                custom.model.names = c("b (SE)",
                                       "OR [95 CI]"),
                caption = "Hoffman's EXAMPLE 3.2 A Loistic Regression Model of Gender and Life Satisfaction, top of page 51",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4,
                ci.test = 1)

Hoffman’s EXAMPLE 3.2 A Loistic Regression Model of Gender and Life Satisfaction, top of page 51
	b (SE)	OR [95 CI]
(Intercept)	0.6931 (0.4629)	2.0000 [0.8322; 5.2772]
sexfemale	-1.1160 (0.5078)^*	0.3276 [0.1148; 0.8625]^*
AIC	159.6205	159.6205
BIC	165.1449	165.1449
Log Likelihood	-77.8103	-77.8103
Deviance	155.6205	155.6205
Num. obs.	117	117
p < 0.001; p < 0.01; p < 0.05 (or Null hypothesis value outside the confidence interval).

10.3.3 Assess Model Fit

10.3.3.1 Likelihood Ratio Test (LRT, aka. Deviance Difference Test)

drop1(fit_glm_1, test = "LRT")

# A tibble: 2 x 5
     Df Deviance   AIC   LRT `Pr(>Chi)`
  <dbl>    <dbl> <dbl> <dbl>      <dbl>
1    NA     156.  160. NA       NA     
2     1     161.  163.  5.13     0.0235

performance::compare_performance(fit_glm_1)

# A tibble: 1 x 11
  Model Type    AIC   BIC R2_Tjur  RMSE LOGLOSS SCORE_LOG SCORE_SPHERICAL   PCP
  <chr> <chr> <dbl> <dbl>   <dbl> <dbl>   <dbl>     <dbl>           <dbl> <dbl>
1 fit_~ glm    160.  165.  0.0437  1.15   0.665     -30.1          0.0550 0.528
# ... with 1 more variable: BF <dbl>

10.3.3.2 R-squared “like” measures

performance::r2(fit_glm_1)

$R2_Tjur
Tjur's R2 
  0.04375

performance::r2_mcfadden(fit_glm_1)

# R2 for Generalized Linear Regression

       R2: 0.032
  adj. R2: 0.019

performance::r2_nagelkerke(fit_glm_1)

Nagelkerke's R2 
     0.05742029

pscl::pR2(fit_glm_1)

fitting null model for pseudo-r2

         llh      llhNull           G2     McFadden         r2ML         r2CU 
-77.81025523 -80.37450446   5.12849846   0.03190376   0.04288652   0.05742029

10.3.4 Plot Predicted Probabilitites

sjPlot::plot_model(model = fit_glm_1,
                   type = "pred")

$sex

10.3.4.1 Logit scale

fit_glm_1 %>% 
  emmeans::emmeans(~ sex)

 sex    emmean    SE  df asymp.LCL asymp.UCL
 male    0.693 0.463 Inf    -0.214    1.6004
 female -0.423 0.209 Inf    -0.832   -0.0138

Results are given on the logit (not the response) scale. 
Confidence level used: 0.95

fit_glm_1 %>% 
  emmeans::emmeans(~ sex) %>% 
  pairs()

 contrast      estimate    SE  df z.ratio p.value
 male - female     1.12 0.508 Inf 2.198   0.0280 

Results are given on the log odds ratio (not the response) scale.

10.3.4.2 Response Scale (probability)

fit_glm_1 %>% 
  emmeans::emmeans(~ sex,
                   type = "response")

 sex     prob     SE  df asymp.LCL asymp.UCL
 male   0.667 0.1029 Inf     0.447     0.832
 female 0.396 0.0499 Inf     0.303     0.497

Confidence level used: 0.95 
Intervals are back-transformed from the logit scale

fit_glm_1 %>% 
  emmeans::emmeans(~ sex,
                   type = "response") %>% 
  pairs()

 contrast      odds.ratio   SE  df z.ratio p.value
 male / female       3.05 1.55 Inf 2.198   0.0280 

Tests are performed on the log odds ratio scale

10.3.5 Interpretation

On average, two out of every three males is depressed, b = 0.667, odds = 1.95, 95% CI [1.58, 2.40].
Females have nearly a quarter lower odds of being depressed, compared to men, b = -0.27, OR = 0.77, 95% IC [0.61, 0.96], p = .028.

10.3.6 Diagnostics

10.3.6.1 Influential values

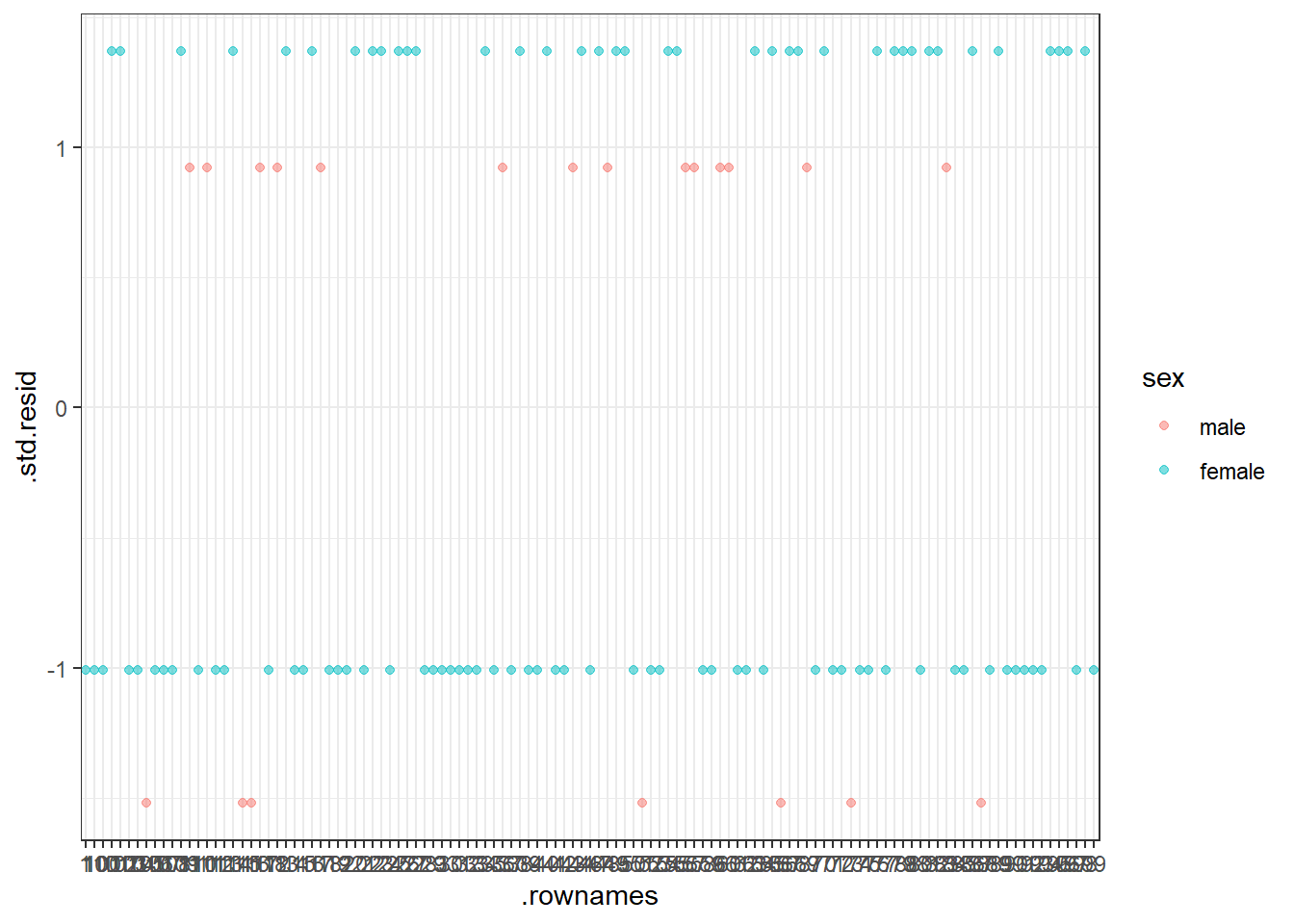
Influential values are extreme individual data points that can alter the quality of the logistic regression model.

The most extreme values in the data can be examined by visualizing the Cook’s distance values. Here we label the top 7 largest values:

plot(fit_glm_1, which = 4, id.n = 7)

Note that, not all outliers are influential observations. To check whether the data contains potential influential observations, the standardized residual error can be inspected. Data points with an absolute standardized residuals above 3 represent possible outliers and may deserve closer attention.

10.3.6.2 Standardized Residuals

The following R code computes the standardized residuals (.std.resid) using the R function augment() [broom package].

fit_glm_1 %>% 
  broom::augment() %>% 
  ggplot(aes(x = .rownames, .std.resid)) + 
  geom_point(aes(color = sex), alpha = .5) +
  theme_bw()

10.4 Logisitic Regression Model 2: many IV’s

10.4.1 Fit the Model

fit_glm_2 <- glm(satlife ~ sex + iq + age + weight,
                 data = df_depress,
                 family = binomial(link = "logit"))

fit_glm_2 %>% summary() %>% coef()

               Estimate Std. Error    z value   Pr(>|z|)
(Intercept)  9.02054236 6.01858970  1.4987801 0.13393069
sexfemale   -1.27924381 0.55971456 -2.2855289 0.02228183
iq          -0.07279837 0.05361036 -1.3579161 0.17449031
age         -0.04112838 0.05250052 -0.7833900 0.43339814
weight      -0.03768972 0.08885942 -0.4241499 0.67145648

10.4.2 Tabulate Parameters

texreg::knitreg(list(fit_glm_2,
                     texreghelpr::extract_glm_exp(fit_glm_2)),
                custom.model.names = c("b (SE)",
                                       "OR [95 CI]"),
                caption = "EXAMPLE 3.3 A Logistic Regression Model of Life Satisfaction with Multiple Independent Variables, middle of page 52",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4,
                ci.test = 1)

EXAMPLE 3.3 A Logistic Regression Model of Life Satisfaction with Multiple Independent Variables, middle of page 52
	b (SE)	OR [95 CI]
(Intercept)	9.0205 (6.0186)	8271.2619 [0.0854; 2077566352.1374]
sexfemale	-1.2792 (0.5597)^*	0.2782 [0.0870; 0.8060]^*
iq	-0.0728 (0.0536)	0.9298 [0.8327; 1.0304]
age	-0.0411 (0.0525)	0.9597 [0.8635; 1.0627]
weight	-0.0377 (0.0889)	0.9630 [0.8073; 1.1472]
AIC	137.5217	137.5217
BIC	150.4973	150.4973
Log Likelihood	-63.7609	-63.7609
Deviance	127.5217	127.5217
Num. obs.	99	99
p < 0.001; p < 0.01; p < 0.05 (or Null hypothesis value outside the confidence interval).

10.4.3 Assess Model Fit

drop1(fit_glm_2, test = "LRT")

# A tibble: 5 x 5
     Df Deviance   AIC    LRT `Pr(>Chi)`
  <dbl>    <dbl> <dbl>  <dbl>      <dbl>
1    NA     128.  138. NA        NA     
2     1     133.  141.  5.59      0.0180
3     1     129.  137.  1.91      0.167 
4     1     128.  136.  0.621     0.431 
5     1     128.  136.  0.180     0.671

10.4.4 Variance Explained

performance::compare_performance(fit_glm_2)

# A tibble: 1 x 11
  Model Type    AIC   BIC R2_Tjur  RMSE LOGLOSS SCORE_LOG SCORE_SPHERICAL   PCP
  <chr> <chr> <dbl> <dbl>   <dbl> <dbl>   <dbl>     <dbl>           <dbl> <dbl>
1 fit_~ glm    138.  150.  0.0753  1.13   0.644     -23.1          0.0220 0.548
# ... with 1 more variable: BF <dbl>

10.4.4.1 R-squared “lik” measures

performance::r2_nagelkerke(fit_glm_2)

Nagelkerke's R2 
     0.09728404

10.4.5 Diagnostics

10.4.5.1 Multicollinearity

Multicollinearity corresponds to a situation where the data contain highly correlated predictor variables. Read more in Chapter (???)(multicollinearity).

Multicollinearity is an important issue in regression analysis and should be fixed by removing the concerned variables. It can be assessed using the R function vif() [car package], which computes the variance inflation factors:

car::vif(fit_glm_2)

     sex       iq      age   weight 
1.011608 1.294334 1.418975 1.233364

As a rule of thumb, a VIF value that exceeds 5 or 10 indicates a problematic amount of collinearity. In our example, there is no collinearity: all variables have a value of VIF well below 5.

10.5 Compare Models

10.5.1 Refit to Complete Cases

Restrict the data to only participant that have all four of these predictors.

df_depress_model <- df_depress %>% 
                        dplyr::filter(complete.cases(sex, iq, age, weight))

Refit Model 1 with only participant complete on all the predictors.

fit_glm_1_redo <- glm(satlife ~ sex,
                      data = df_depress_model)

fit_glm_2_redo <- glm(satlife ~ sex + iq + age + weight,
                      data = df_depress_model)

texreg::knitreg(list(texreghelpr::extract_glm_exp(fit_glm_1_redo),
                     texreghelpr::extract_glm_exp(fit_glm_2_redo)),
                custom.model.names = c("Single IV",
                                       "Multiple IVs"),
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4,
                ci.test = 1)

Statistical models
	Single IV	Multiple IVs
(Intercept)	1.9477 [1.5562; 2.4377]^*	12.7108 [0.8969; 180.1414]
sexfemale	0.7436 [0.5802; 0.9529]^*	0.7388 [0.5755; 0.9483]^*
iq		0.9837 [0.9606; 1.0074]
age		0.9908 [0.9677; 1.0144]
weight		0.9913 [0.9521; 1.0322]
AIC	141.9675	145.7895
BIC	149.7528	161.3602
Log Likelihood	-67.9837	-66.8948
Deviance	22.8889	22.3908
Num. obs.	99	99
^* Null hypothesis value outside the confidence interval.

anova(fit_glm_1_redo, 
      fit_glm_2_redo,
      test = "LRT")

# A tibble: 2 x 5
  `Resid. Df` `Resid. Dev`    Df Deviance `Pr(>Chi)`
        <dbl>        <dbl> <dbl>    <dbl>      <dbl>
1          97         22.9    NA   NA         NA    
2          94         22.4     3    0.498      0.554

performance::compare_performance(fit_glm_1_redo, 
                                 fit_glm_2_redo, 
                                 rank = TRUE)

# A tibble: 2 x 8
  Model          Type    AIC   BIC R2_Nagelkerke  RMSE      BF Performance_Score
  <chr>          <chr> <dbl> <dbl>         <dbl> <dbl>   <dbl>             <dbl>
1 fit_glm_1_redo glm    142.  150.        0.0599 0.481 1                     0.6
2 fit_glm_2_redo glm    146.  161.        0.0827 0.476 0.00302               0.4

10.5.2 Interpretation

Only sex is predictive of depression. There is no evidence IQ, age, or weight are associated with depression, all p’s > .16.