13 Ordered Logistic Regression - Ex: Spaking

library(tidyverse)
library(haven)        # read in SPSS dataset
library(furniture)    # nice table1() descriptives
library(stargazer)    # display nice tables: summary & regression
library(texreg)       # Convert Regression Output to LaTeX or HTML Tables
library(psych)        # contains some useful functions, like headTail
library(car)          # Companion to Applied Regression
library(sjPlot)       # Quick plots and tables for models
library(car)          # Companion to Applied Regression (a text book - includes datasets)
library(MASS)         # Support Functions and Datasets
library(nnet)         #  Multinomial Log-Linear Models
library(pscl)         # Political Science Computational Laboratory (ZIP)

13.1 Background

This dataset comes from John Hoffman’s textbook: Regression Models for Categorical, Count, and Related Variables: An Applied Approach (2004) Amazon link, 2014 edition

Chapter 4: Ordered Logistic and Probit Regression Models

Dataset: The following example uses the SPSS data set gss.sav. The dependent variable of interest is labeled spanking.

" The pertinent question (spanking) asks “Do you strongly agree, agree, disagree, or strongly disagree that it is sometimes necessary to discipline a child with a good, hard spanking?” The possible answers are coded as 1 = strongly agree, 2 = agree, 3 = disagree, and 4 = strongly disagree. A common hypothesis is that support for corporal punishment of children decreases at higher levels of education."

13.1.1 Raw Dataset

data_gss <- haven::read_spss("https://raw.githubusercontent.com/CEHS-research/data/master/Hoffmann_datasets/gss.sav") %>% 
  haven::as_factor()

data_gss %>% 
  dplyr::select(spanking, female, nonwhite, educate, income) %>% 
  dplyr::filter(!is.na(spanking)) %>%      # about 1/3 of participants are missing this
  head()

# A tibble: 6 x 5
  spanking female nonwhite  educate income
  <fct>    <fct>  <fct>       <dbl>  <dbl>
1 agree    male   white          16     12
2 agree    female white          11      2
3 disagree male   white          15     12
4 disagree male   white          14     NA
5 agree    female non-white      16     12
6 agree    male   white          12     NA

13.1.2 Wrangle Data

data_gss_model <- data_gss %>% 
  dplyr::mutate(spankingN = as.numeric(spanking)) %>%   # numeric version: 1, 2, 3, 4
  dplyr::mutate(polviewsN = as.numeric(polviews)) %>% 
  dplyr::filter(complete.cases(educate, spanking))      # only include complete cases

13.2 Exploratory Data Analysis

13.2.1 Entire Sample

data_gss %>% 
  furniture::table1(spanking,
                    na.rm = FALSE,
                    output = "markdown",
                    caption = "Hoffmann's Example 4.1 Summary of the Spanking Variable")

Table 13.1: Hoffmann’s Example 4.1 Summary of the Spanking Variable
	Mean/Count (SD/%)
	n = 2903
spanking
strongly agree	512 (17.6%)
agree	890 (30.7%)
disagree	357 (12.3%)
strongly disagree	164 (5.6%)
NA	980 (33.8%)

data_gss %>% 
  ggplot(aes(spanking)) +
  geom_bar()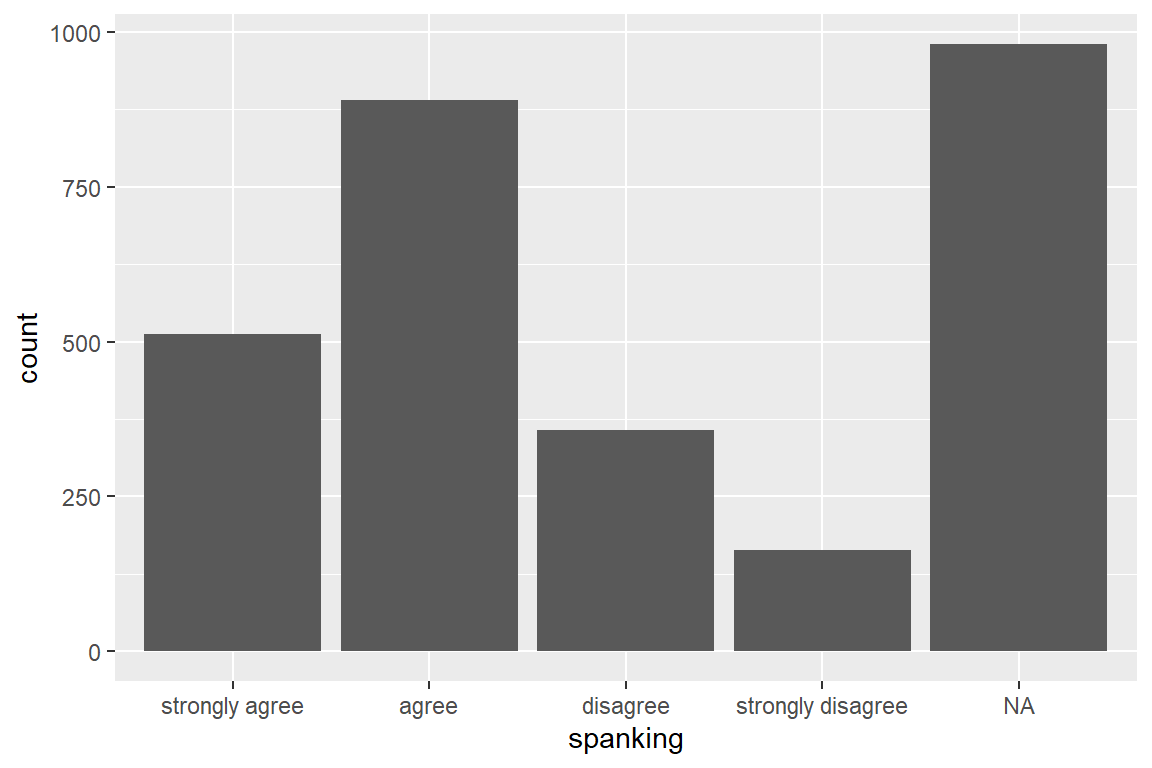

13.2.2 By Education

data_gss %>% 
  dplyr::group_by(forcats::fct_explicit_na(spanking)) %>% 
  furniture::table1("Educations, years" = educate,
                    "Education, factor" = factor(educate),
                    na.rm  = FALSE,
                    digits = 2,
                    output = "markdown")

	strongly agree	agree	disagree	strongly disagree	(Missing)
	n = 512	n = 890	n = 357	n = 164	n = 980
Educations, years
	12.64 (2.96)	13.40 (2.84)	14.00 (2.74)	14.24 (3.00)	13.32 (2.95)
Education, factor
0	0 (0%)	2 (0.2%)	0 (0%)	0 (0%)	2 (0.2%)
3	5 (1%)	0 (0%)	0 (0%)	0 (0%)	3 (0.3%)
4	1 (0.2%)	0 (0%)	0 (0%)	1 (0.6%)	4 (0.4%)
5	4 (0.8%)	5 (0.6%)	0 (0%)	1 (0.6%)	3 (0.3%)
6	5 (1%)	5 (0.6%)	1 (0.3%)	0 (0%)	3 (0.3%)
7	7 (1.4%)	8 (0.9%)	0 (0%)	1 (0.6%)	7 (0.7%)
8	25 (4.9%)	15 (1.7%)	5 (1.4%)	2 (1.2%)	33 (3.4%)
9	15 (2.9%)	20 (2.2%)	7 (2%)	4 (2.4%)	23 (2.3%)
10	27 (5.3%)	44 (4.9%)	11 (3.1%)	4 (2.4%)	35 (3.6%)
11	39 (7.6%)	42 (4.7%)	16 (4.5%)	5 (3%)	53 (5.4%)
12	152 (29.7%)	270 (30.3%)	97 (27.2%)	33 (20.1%)	297 (30.3%)
13	56 (10.9%)	90 (10.1%)	41 (11.5%)	19 (11.6%)	90 (9.2%)
14	56 (10.9%)	111 (12.5%)	41 (11.5%)	19 (11.6%)	112 (11.4%)
15	19 (3.7%)	47 (5.3%)	14 (3.9%)	14 (8.5%)	59 (6%)
16	59 (11.5%)	105 (11.8%)	68 (19%)	31 (18.9%)	129 (13.2%)
17	13 (2.5%)	45 (5.1%)	14 (3.9%)	6 (3.7%)	42 (4.3%)
18	17 (3.3%)	43 (4.8%)	15 (4.2%)	11 (6.7%)	39 (4%)
19	3 (0.6%)	15 (1.7%)	8 (2.2%)	2 (1.2%)	13 (1.3%)
20	8 (1.6%)	20 (2.2%)	18 (5%)	11 (6.7%)	29 (3%)
NA	1 (0.2%)	3 (0.3%)	1 (0.3%)	0 (0%)	4 (0.4%)

13.2.3 Spanking by Sex

data_gss %>% 
  dplyr::filter(complete.cases(female, spanking)) %>% 
  dplyr::select(female, spanking) %>% 
  table() %>% 
  addmargins()

        spanking
female   strongly agree agree disagree strongly disagree  Sum
  male              243   388      156                56  843
  female            269   502      201               108 1080
  Sum               512   890      357               164 1923

data_gss %>% 
  dplyr::filter(complete.cases(female, spanking)) %>%  
  furniture::tableX(female, spanking,
                    type = "count")

        spanking
female   strongly agree agree disagree strongly disagree Total
  male   243            388   156      56                843  
  female 269            502   201      108               1080 
  Total  512            890   357      164               1923

data_gss %>% 
  dplyr::filter(complete.cases(female, spanking)) %>%  
  furniture::tableX(female, spanking,
                    type = "row_perc")

        spanking
female   strongly agree agree disagree strongly disagree Total 
  male   28.83          46.03 18.51    6.64              100.00
  female 24.91          46.48 18.61    10.00             100.00
  All    26.63          46.28 18.56    8.53              100.00

data_gss %>% 
  dplyr::filter(complete.cases(female, spanking)) %>%  
  furniture::tableX(female, spanking,
                    type = "col_perc")

        spanking
female   strongly agree agree  disagree strongly disagree All   
  male   47.46          43.60  43.70    34.15             43.84 
  female 52.54          56.40  56.30    65.85             56.16 
  Total  100.00         100.00 100.00   100.00            100.00

data_gss %>% 
  dplyr::filter(complete.cases(female, spanking)) %>%  
  furniture::tableX(female, spanking,
                    type = "cell_perc")

        spanking
female   strongly agree agree disagree strongly disagree Total 
  male   12.64          20.18 8.11     2.91              43.84 
  female 13.99          26.11 10.45    5.62              56.16 
  Total  26.63          46.28 18.56    8.53              100.00

data_gss %>% 
  dplyr::filter(complete.cases(female, spanking)) %>%   
  dplyr::group_by(spanking) %>% 
  furniture::table1(female)


--------------------------------------------------------------------
                                 spanking 
           strongly agree agree       disagree    strongly disagree
           n = 512        n = 890     n = 357     n = 164          
 female                                                            
    male   243 (47.5%)    388 (43.6%) 156 (43.7%) 56 (34.1%)       
    female 269 (52.5%)    502 (56.4%) 201 (56.3%) 108 (65.9%)      
--------------------------------------------------------------------

13.3 Linear Regression

Linear regression is often ill-suited to fitting a likert rating, such as agreement.

13.3.1 Visualization

data_gss_model %>% 
  ggplot(aes(x = educate,
             y = spankingN)) +                    
  geom_count() +                               # point size relative to over-plotting
  geom_smooth(method = "lm") +                 # add linear regression line (OLS)
  theme_bw() +
  labs(x = "Years of Formal Education",
       y = "Spanking")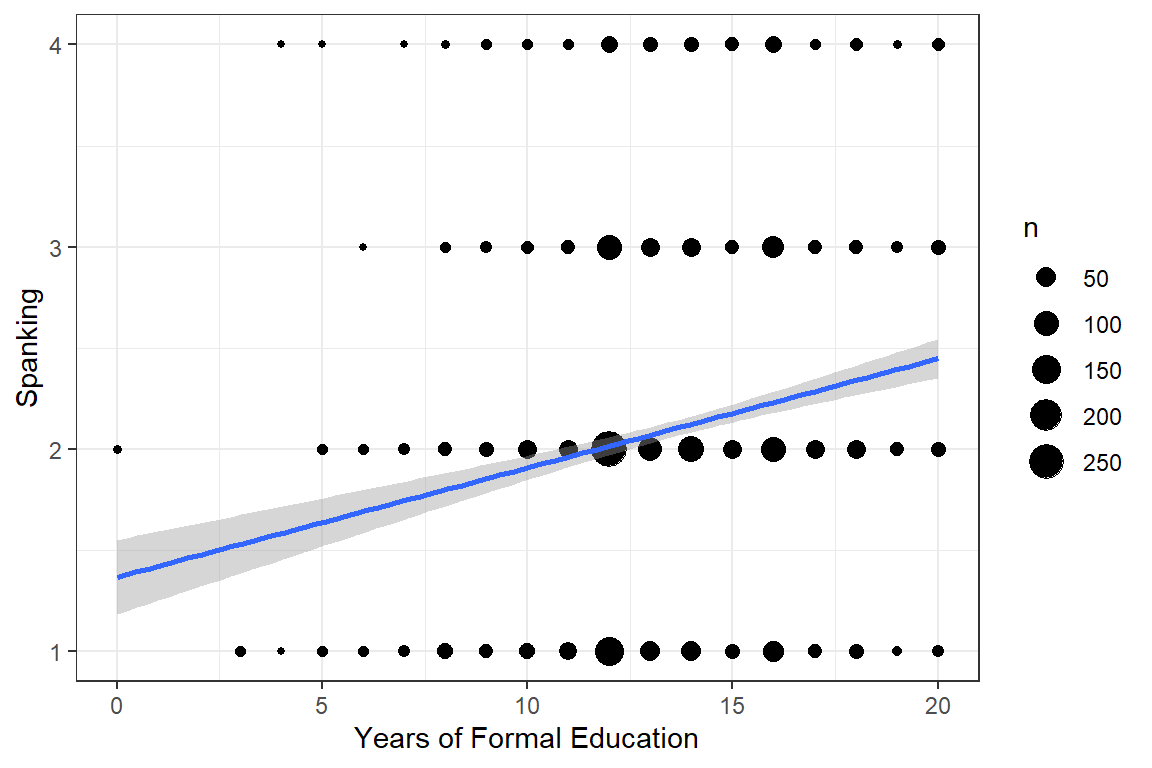

Figure 13.1: Hoffmann’s Figure 4.1

13.3.2 Fit the Model

fit_lm <- lm(spankingN ~ educate,
             data = data_gss_model)

summary(fit_lm)


Call:
lm(formula = spankingN ~ educate, data = data_gss_model)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.44768 -0.79947 -0.06955  0.66036  2.41660 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.367326   0.093670  14.597  < 2e-16 ***
educate     0.054018   0.006839   7.898 4.73e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.8729 on 1916 degrees of freedom
Multiple R-squared:  0.03153,   Adjusted R-squared:  0.03103 
F-statistic: 62.38 on 1 and 1916 DF,  p-value: 4.73e-15

anova(fit_lm)

# A tibble: 2 x 5
     Df `Sum Sq` `Mean Sq` `F value`  `Pr(>F)`
  <int>    <dbl>     <dbl>     <dbl>     <dbl>
1     1     47.5    47.5        62.4  4.73e-15
2  1916   1460.      0.762      NA   NA

13.3.3 Tabulate Parameters

texreg::knitreg(fit_lm,
                custom.model.name = "Linear Regression",
                caption = "Hoffmann's Example 4.2",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4)

Hoffmann’s Example 4.2
	Linear Regression
(Intercept)	1.3673 (0.0937)^***
educate	0.0540 (0.0068)^***
R²	0.0315
Adj. R²	0.0310
Num. obs.	1918
p < 0.001; p < 0.01; p < 0.05

13.3.4 Model Fit and Variance Explained

performance::performance(fit_lm)

# A tibble: 1 x 6
    AIC   BIC     R2 R2_adjusted  RMSE Sigma
  <dbl> <dbl>  <dbl>       <dbl> <dbl> <dbl>
1 4926. 4942. 0.0315      0.0310 0.872 0.873

performance::r2(fit_lm)

# R2 for Linear Regression
       R2: 0.032
  adj. R2: 0.031

13.3.5 Residual Diagnostics

sjPlot::plot_model(fit_lm, type = "diag")

[[1]]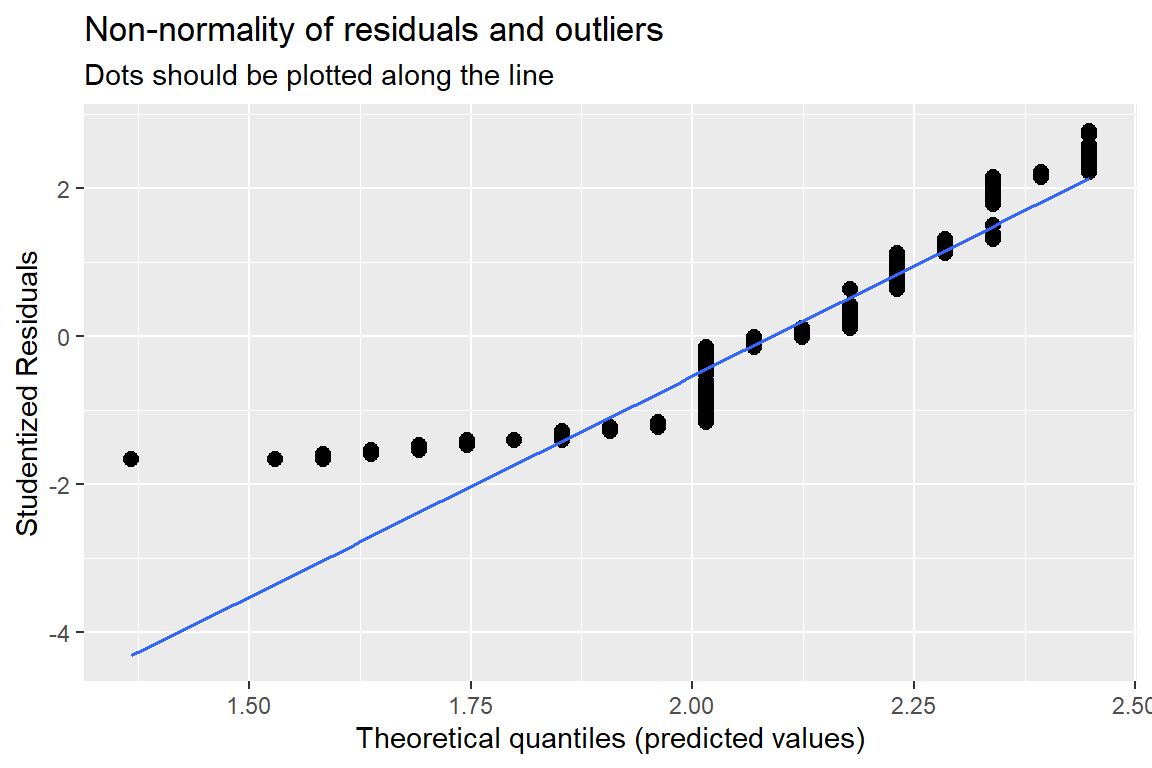

Figure 13.2: Hoffman’s Figures 4.2 adn 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK!


[[2]]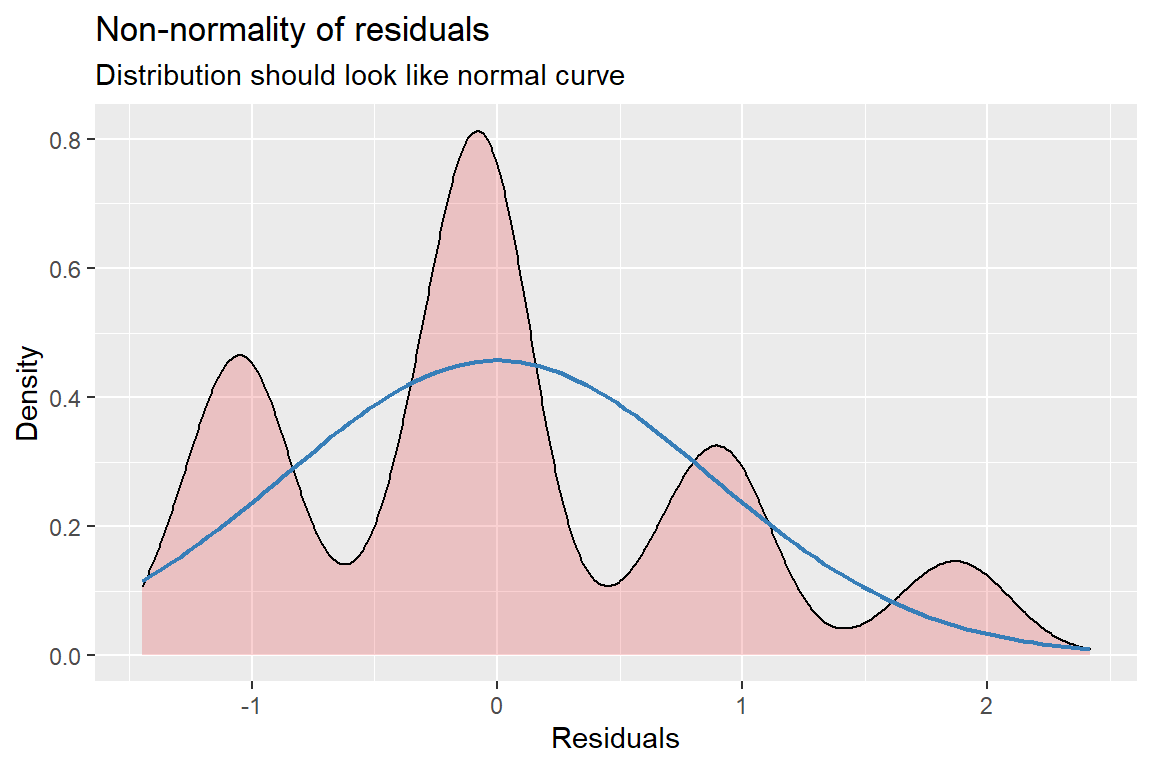

Figure 13.3: Hoffman’s Figures 4.2 adn 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK!


[[3]]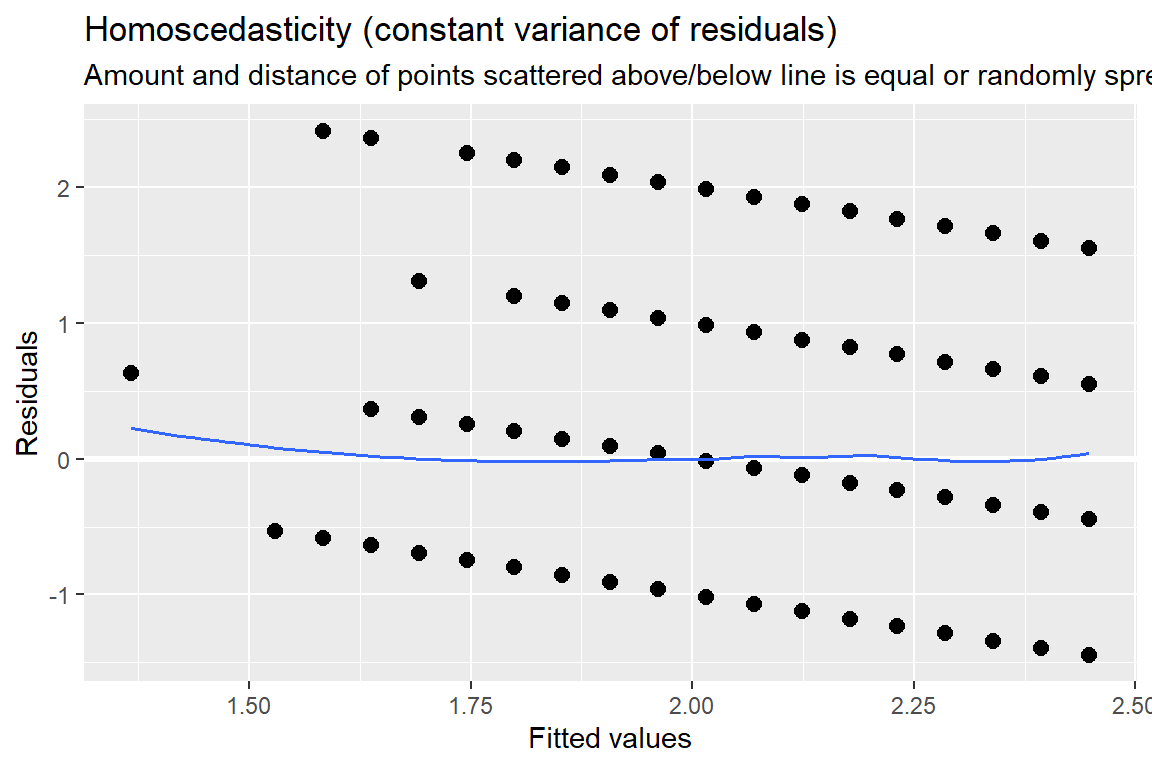

Figure 13.4: Hoffman’s Figures 4.2 adn 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK!

13.4 Ordered Logistic Regression

data_gss_model %>% 
  dplyr::group_by(forcats::fct_explicit_na(spanking)) %>% 
  furniture::table1("Sex" = female,
                    caption = "Hoffmann's Example 4.3 Crosstabulate DV with Sex",
                    na.rm  = FALSE,
                    digits = 2,
                    total = TRUE,
                    output = "markdown")

Table 13.2: Hoffmann’s Example 4.3 Crosstabulate DV with Sex
	Total	strongly agree	agree	disagree	strongly disagree
	n = 1918	n = 511	n = 887	n = 356	n = 164
Sex
male	841 (43.8%)	243 (47.6%)	387 (43.6%)	155 (43.5%)	56 (34.1%)
female	1077 (56.2%)	268 (52.4%)	500 (56.4%)	201 (56.5%)	108 (65.9%)
NA	0 (0%)	0 (0%)	0 (0%)	0 (0%)	0 (0%)

data_gss_model %>% 
  furniture::tableX(female, spanking)

        spanking
female   strongly agree agree disagree strongly disagree Total
  male   243            387   155      56                841  
  female 268            500   201      108               1077 
  Total  511            887   356      164               1918

13.5 Proportional-odds (ordinal) Logistic Regression

This type of logisit regression model forces the predictors to have similar relationship with the outcome (slopes), but different means (intercepts). This is called the proportional odds assumption.

13.5.1 Fit Model 1: Sex

Use polr() function in the base \(R\) MASS package. While outcome variable (dependent variable, “Y”) may be a regular factor, it is preferable to specify it as an ordered factor.

fit_polr_1 <- MASS::polr(spanking ~ female,
                         data = data_gss_model)

summary(fit_polr_1)

Call:
MASS::polr(formula = spanking ~ female, data = data_gss_model)

Coefficients:
              Value Std. Error t value
femalefemale 0.2116    0.08532    2.48

Intercepts:
                           Value    Std. Error t value 
strongly agree|agree        -0.8967   0.0694   -12.9114
agree|disagree               1.1094   0.0711    15.6078
disagree|strongly disagree   2.4922   0.0958    26.0026

Residual Deviance: 4719.394 
AIC: 4727.394

13.5.2 Extract Parameters

13.5.2.1 Logit Scale

fit_polr_1$zeta

      strongly agree|agree             agree|disagree 
                -0.8966862                  1.1093754 
disagree|strongly disagree 
                 2.4921855

fit_polr_1 %>% coef()

femalefemale 
   0.2116244

fit_polr_1 %>% confint()

     2.5 %     97.5 % 
0.04451894 0.37901780

13.5.2.2 Odds-Ratio Scale

fit_polr_1$zeta %>% exp()

      strongly agree|agree             agree|disagree 
                 0.4079192                  3.0324638 
disagree|strongly disagree 
                12.0876653

fit_polr_1 %>% coef() %>% exp()

femalefemale 
    1.235684

fit_polr_1 %>% confint() %>% exp()

   2.5 %   97.5 % 
1.045525 1.460849

13.5.2.3 Predicted Probabilities

effects::allEffects(fit_polr_1)

 model: spanking ~ female

female effect (probability) for strongly agree
female
    male   female 
0.289732 0.248186 

female effect (probability) for agree
female
     male    female 
0.4622807 0.4623011 

female effect (probability) for disagree
female
     male    female 
0.1715795 0.1967672 

female effect (probability) for strongly disagree
female
      male     female 
0.07640782 0.09274572

13.5.3 Tabulate parameters

texreg::knitreg(fit_polr_1,
                custom.model.name = c("b (SE)"),
                custom.coef.map = list("femalefemale"             = "Female vs. Male",
                                       "strongly agree|agree"     = "strongly agree|agree",
                                       "agree|disagree"           = "agree|disagree",
                                       "disagree|strongly disagree" = "disagree|strongly disagree"),
                groups = list("Predictors" = 1,
                              "Cut Values (i.e. threasholds)" = 2:4),
                caption = "Hoffmann's Example 4.4 Ordered Logistic Regression",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4)

Hoffmann’s Example 4.4 Ordered Logistic Regression
	b (SE)
Predictors
Female vs. Male	0.2116 (0.0853)^*
Cut Values (i.e. threasholds)
strongly agree\|agree	-0.8967 (0.0694)^***
agree\|disagree	1.1094 (0.0711)^***
disagree\|strongly disagree	2.4922 (0.0958)^***
AIC	4727.3944
BIC	4749.6306
Log Likelihood	-2359.6972
Deviance	4719.3944
Num. obs.	1918
p < 0.001; p < 0.01; p < 0.05

13.5.4 Predicted Probabilities

ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female"))

# A tibble: 8 x 7
  x      response.level    predicted std.error conf.low conf.high group
  <fct>  <chr>                 <dbl>     <dbl>    <dbl>     <dbl> <fct>
1 male   strongly.agree       0.290     0.0694   0.263     0.319  1    
2 female strongly.agree       0.248     0.0647   0.225     0.273  1    
3 male   agree                0.462     0.0460   0.440     0.485  1    
4 female agree                0.462     0.0459   0.440     0.485  1    
5 male   disagree             0.172     0.0708   0.153     0.192  1    
6 female disagree             0.197     0.0653   0.177     0.218  1    
7 male   strongly.disagree    0.0764    0.0958   0.0642    0.0908 1    
8 female strongly.disagree    0.0927    0.0889   0.0791    0.108  1

ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female")) %>% 
  dplyr::filter(x == "female")

# A tibble: 4 x 7
  x      response.level    predicted std.error conf.low conf.high group
  <fct>  <chr>                 <dbl>     <dbl>    <dbl>     <dbl> <fct>
1 female strongly.agree       0.248     0.0647   0.225      0.273 1    
2 female agree                0.462     0.0459   0.440      0.485 1    
3 female disagree             0.197     0.0653   0.177      0.218 1    
4 female strongly.disagree    0.0927    0.0889   0.0791     0.108 1

13.5.5 Plot Predicted Probabilities

ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female")) %>%    # x-axis
  data.frame() %>% 
  ggplot(aes(x = x,
             y = predicted,
             group = response.level,
             color = response.level)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .25) +
  geom_point(size = 4) +
  geom_line(aes(linetype = response.level))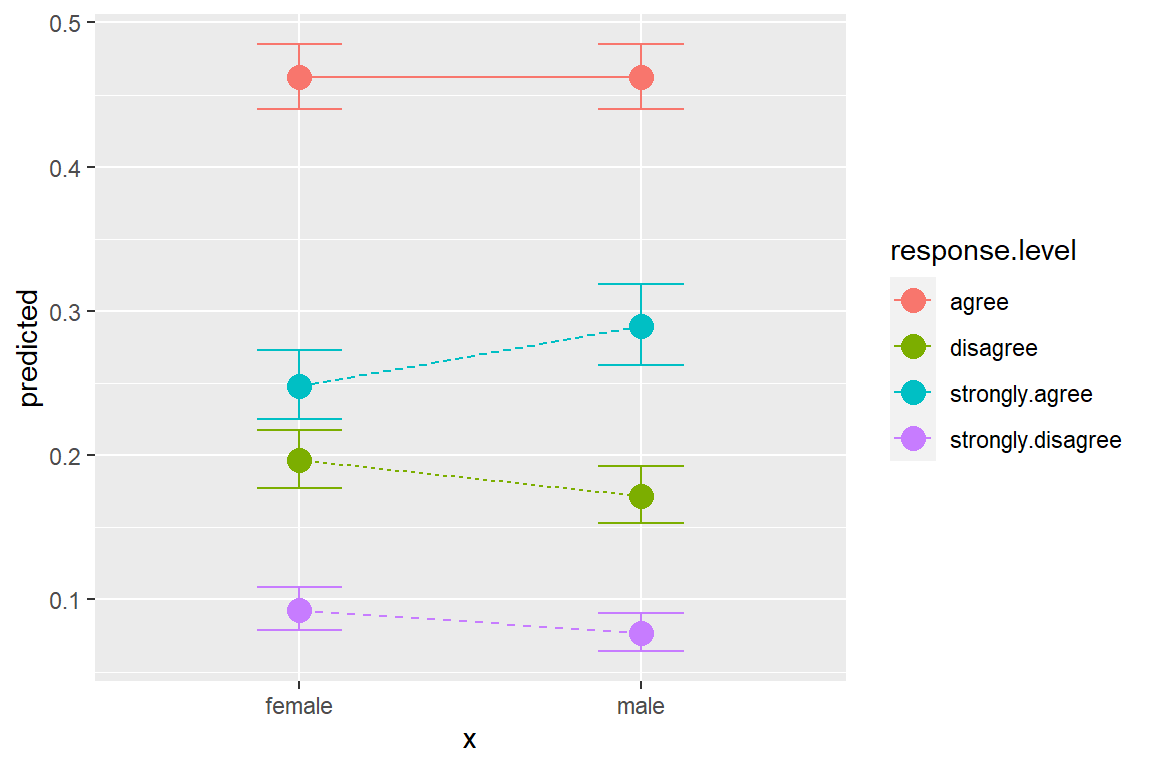

ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female")) %>%    # x-axis
  data.frame() %>% 
  dplyr::mutate(response.level = response.level %>% 
                  forcats::fct_reorder(predicted) %>% 
                  forcats::fct_rev()) %>% 
  ggplot(aes(x = x,
             y = predicted,
             group = response.level,
             color = response.level)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .25) +
  geom_point(size = 4) +
  geom_line(aes(linetype = response.level)) +
  theme_bw() +
  labs(x = NULL,
       y = "Predicted Probability",
       color    = "Spanking:",
       shape    = "Spanking:",
       linetype = "Spanking:") +
  theme(legend.key.width = unit(2, "cm")) +
  scale_linetype_manual(values = c("solid", "longdash", "dotdash", "dotted")) +
  scale_shape_manual(values = c(0, 1, 2, 8))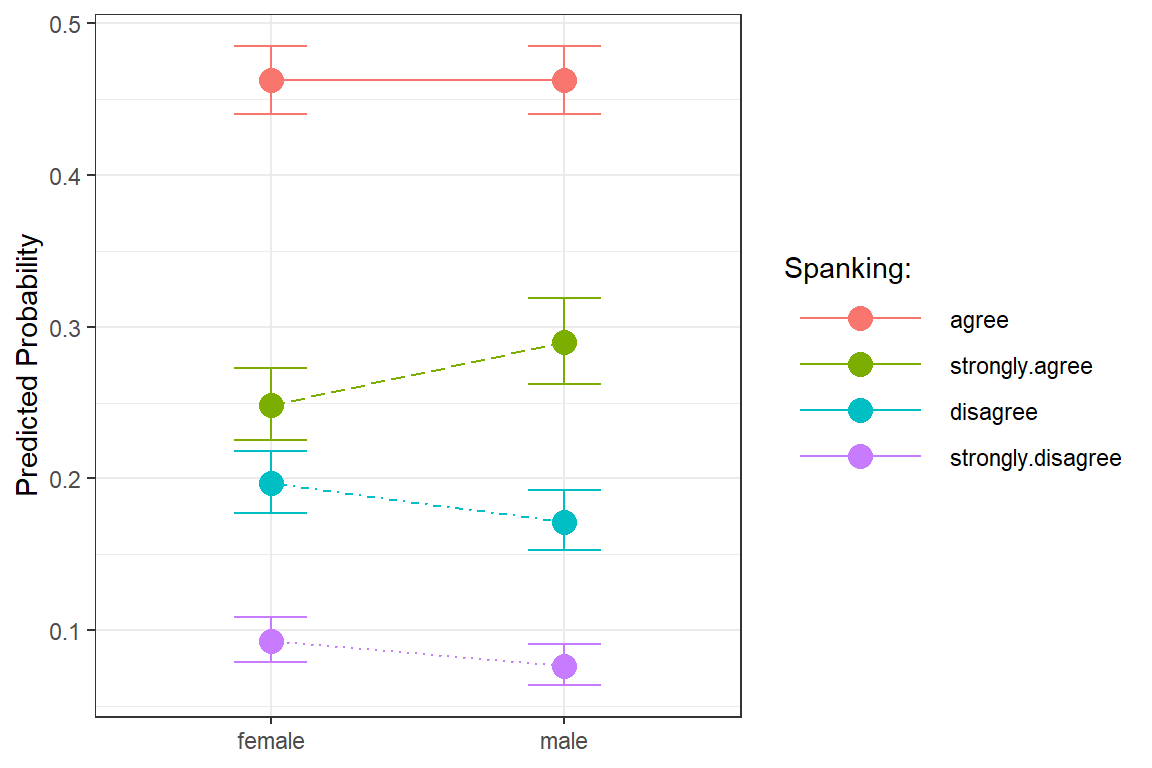

13.5.6 Model Fit and Variance Explained

fit_polr_0 <- MASS::polr(spanking ~ 1,
                         data = data_gss_model)

anova(fit_polr_1, fit_polr_0)

# A tibble: 2 x 7
  Model  `Resid. df` `Resid. Dev` Test     `   Df` `LR stat.` `Pr(Chi)`
  <chr>        <dbl>        <dbl> <chr>      <dbl>      <dbl>     <dbl>
1 1             1915        4726. ""            NA      NA      NA     
2 female        1914        4719. "1 vs 2"       1       6.16    0.0130

performance::performance(fit_polr_1)

Can't calculate log-loss.
Can't calculate proper scoring rules for ordinal, multinomial or cumulative link models.

# A tibble: 1 x 5
    AIC   BIC R2_Nagelkerke  RMSE Sigma
  <dbl> <dbl>         <dbl> <dbl> <dbl>
1 4727. 4750.       0.00351  2.05  1.57

performance::r2(fit_polr_1)

  Nagelkerke's R2: 0.004

13.5.7 Assumptions

13.5.7.1 Proportional Odds: Brant Test

The poTest function implements tests proposed by Brant (1990) for proportional odds for logistic models fit by the polr() function in the MASS package.

# Hoffmann's Examle 4.5 (continued...)
car::poTest(fit_polr_1)


Tests for Proportional Odds
MASS::polr(formula = spanking ~ female, data = data_gss_model)

             b[polr] b[>strongly agree] b[>agree] b[>disagree] Chisquare df
Overall                                                             3.01  2
femalefemale   0.212              0.204     0.183        0.446      3.01  2
             Pr(>Chisq)
Overall            0.22
femalefemale       0.22

A significant test statistics provides evidence that the parallel regression assumption has been violated!

13.5.8 Fit Model 2: Sex + Covars

fit_polr_2 <- MASS::polr(spanking ~ female + educate + polviewsN,
                         data = data_gss_model)

summary(fit_polr_2)

Call:
MASS::polr(formula = spanking ~ female + educate + polviewsN, 
    data = data_gss_model)

Coefficients:
               Value Std. Error t value
femalefemale  0.2532    0.08825   2.869
educate       0.1153    0.01564   7.374
polviewsN    -0.2215    0.03248  -6.818

Intercepts:
                           Value   Std. Error t value
strongly agree|agree       -0.2977  0.2671    -1.1146
agree|disagree              1.7845  0.2706     6.5935
disagree|strongly disagree  3.1926  0.2793    11.4312

Residual Deviance: 4396.504 
AIC: 4408.504 
(97 observations deleted due to missingness)

13.5.9 Extract Parameters

13.5.9.1 Logit Scale

fit_polr_2$zeta

      strongly agree|agree             agree|disagree 
                -0.2976843                  1.7844863 
disagree|strongly disagree 
                 3.1926342

fit_polr_2 %>% coef()

femalefemale      educate    polviewsN 
   0.2532132    0.1152980   -0.2214577

fit_polr_2 %>% confint()

                   2.5 %     97.5 %
femalefemale  0.08039420  0.4263963
educate       0.08472724  0.1460403
polviewsN    -0.28526298 -0.1579046

13.5.9.2 Odds-Ratio Scale

fit_polr_2$zeta %>% exp()

      strongly agree|agree             agree|disagree 
                 0.7425358                  5.9565193 
disagree|strongly disagree 
                24.3524926

fit_polr_2 %>% coef() %>% exp()

femalefemale      educate    polviewsN 
   1.2881578    1.1222079    0.8013498

fit_polr_2 %>% confint() %>% exp()

                 2.5 %    97.5 %
femalefemale 1.0837142 1.5317277
educate      1.0884202 1.1572429
polviewsN    0.7518165 0.8539312

13.5.10 Tabulate parameters

texreg::knitreg(fit_polr_2,
                custom.model.name = c("b (SE)"),
                custom.coef.map = list("femalefemale"             = "Female vs. Male",
                                       "educate"                  = "Years of Education",
                                       "polviewsN"                = "Level of Polytical Views",
                                       "strongly agree|agree"     = "strongly agree|agree",
                                       "agree|disagree"           = "agree|disagree",
                                       "disagree|strongly disagree" = "disagree|strongly disagree"),
                groups = list("Predictors" = 1:3,
                              "Cut Values" = 4:6),
                caption = "Hoffmann's Example 4.7 Ordered Logistic Regression",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4)

Hoffmann’s Example 4.7 Ordered Logistic Regression
	b (SE)
Predictors
Female vs. Male	0.2532 (0.0883)^**
Years of Education	0.1153 (0.0156)^***
Level of Polytical Views	-0.2215 (0.0325)^***
Cut Values
strongly agree\|agree	-0.2977 (0.2671)
agree\|disagree	1.7845 (0.2706)^***
disagree\|strongly disagree	3.1926 (0.2793)^***
AIC	4408.5038
BIC	4441.5466
Log Likelihood	-2198.2519
Deviance	4396.5038
Num. obs.	1821
p < 0.001; p < 0.01; p < 0.05

13.5.11 Predicted Probabilities

The ggeffects package computes estimated marginal means (predicted values) for the response, at the margin of specific values or levels from certain model terms, i.e. it generates predictions by a model by holding the non-focal variables constant and varying the focal variable(s).

ggpredict() uses predict() for generating predictions
- factors: uses the reference level
ggeffect() computes marginal effects by internally calling effects::Effect()
- factors: compute a kind of “average” value, which represents the proportions of each factor’s category
ggemmeans() uses emmeans::emmeans()
- factors: compute a kind of “average” value, which represents the proportions of each factor’s category

Use condition to set a specific level for factors in ggemmeans(), so factors are not averaged over their categories, but held constant at a given level.

ggeffects::ggpredict() Adjusted for: * educate = 13.51 The grand mean value * polviewsN = 4.17 The grand mean value

## Hoffmann's Example 4.8 (continues...approximated)
ggeffects::ggpredict(model = fit_polr_2,
                    terms = c("female"))

# A tibble: 8 x 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1 male      0.283      0.253   0.193      0.393 strongly agree    1    
2 male      0.477      0.253   0.357      0.600 agree             1    
3 male      0.169      0.253   0.110      0.250 disagree          1    
4 male      0.0718     0.253   0.0450     0.113 strongly disagree 1    
5 female    0.234      0.276   0.151      0.344 strongly agree    1    
6 female    0.476      0.276   0.346      0.610 agree             1    
7 female    0.199      0.276   0.126      0.299 disagree          1    
8 female    0.0906     0.276   0.0549     0.146 strongly disagree 1

ggeffects::ggpredict(model = fit_polr_2,
                    terms = c("female")) %>% 
  data.frame()

# A tibble: 8 x 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1 male      0.283      0.253   0.193      0.393 strongly agree    1    
2 male      0.477      0.253   0.357      0.600 agree             1    
3 male      0.169      0.253   0.110      0.250 disagree          1    
4 male      0.0718     0.253   0.0450     0.113 strongly disagree 1    
5 female    0.234      0.276   0.151      0.344 strongly agree    1    
6 female    0.476      0.276   0.346      0.610 agree             1    
7 female    0.199      0.276   0.126      0.299 disagree          1    
8 female    0.0906     0.276   0.0549     0.146 strongly disagree 1

13.6 Hoffmann’s Example 4.8 (continues…approximated)

ggeffects::ggpredict() Adjusted for: * female = male The reference category * polviewsN = 4.17 The grand mean value

ggeffects::ggpredict(model = fit_polr_2,
                    terms = c("educate [10, 16]",    # 1st = x
                              "female")) %>%         # 2nd = group
  data.frame() %>% 
  dplyr::filter(group == "male")

# A tibble: 8 x 7
      x predicted std.error conf.low conf.high response.level    group
  <dbl>     <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1    10    0.371      0.209   0.282     0.471  strongly agree    male 
2    10    0.454      0.209   0.356     0.556  agree             male 
3    10    0.125      0.209   0.0868    0.177  disagree          male 
4    10    0.0491     0.209   0.0331    0.0721 strongly disagree male 
5    16    0.228      0.287   0.144     0.342  strongly agree    male 
6    16    0.475      0.287   0.340     0.614  agree             male 
7    16    0.203      0.287   0.127     0.309  disagree          male 
8    16    0.0935     0.287   0.0555    0.153  strongly disagree male

ggeffects::ggeffect() Adjusted for: * female computed a kind of “average” value, which represents the proportions of male/female * polviewsN = 4.17 The grand mean value

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]")) %>% 
  data.frame()

# A tibble: 8 x 7
      x response.level    predicted std.error conf.low conf.high group
  <dbl> <chr>                 <dbl>     <dbl>    <dbl>     <dbl> <fct>
1    10 strongly.agree       0.339     0.0744   0.307     0.372  1    
2    16 strongly.agree       0.204     0.0692   0.183     0.227  1    
3    10 agree                0.465     0.0498   0.441     0.490  1    
4    16 agree                0.469     0.0487   0.445     0.493  1    
5    10 disagree             0.139     0.0793   0.122     0.159  1    
6    16 disagree             0.221     0.0663   0.199     0.244  1    
7    10 strongly.disagree    0.0561    0.105    0.0461    0.0682 1    
8    16 strongly.disagree    0.106     0.0885   0.0908    0.124  1

ggeffects::ggemmeans(model = fit_polr_2,
                     terms = c("educate [10, 16]"),
                     condition = c(female = "female")) %>% 
  data.frame()

# A tibble: 8 x 7
      x predicted std.error conf.low conf.high response.level    group
  <dbl>     <dbl>     <dbl>    <dbl>     <dbl> <fct>             <fct>
1    10    0.314    0.0178    0.279     0.349  strongly agree    1    
2    10    0.472    0.0124    0.448     0.496  agree             1    
3    10    0.151    0.0107    0.130     0.172  disagree          1    
4    10    0.0624   0.00641   0.0498    0.0749 strongly disagree 1    
5    16    0.187    0.0124    0.162     0.211  strongly agree    1    
6    16    0.461    0.0125    0.437     0.486  agree             1    
7    16    0.235    0.0130    0.209     0.260  disagree          1    
8    16    0.117    0.0100    0.0976    0.137  strongly disagree 1

Predictions for specific values: females with 10 or 16 years education

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("female",                 # 1st var = `x`
                              "educate [10, 16]")) %>%  # 2nd var = `group`
  data.frame()

# A tibble: 16 x 7
   x      group response.level    predicted std.error conf.low conf.high
   <fct>  <dbl> <chr>                 <dbl>     <dbl>    <dbl>     <dbl>
 1 male      10 strongly.agree       0.371     0.0909   0.331     0.414 
 2 female    10 strongly.agree       0.314     0.0825   0.281     0.350 
 3 male      16 strongly.agree       0.228     0.0818   0.201     0.258 
 4 female    16 strongly.agree       0.187     0.0820   0.164     0.212 
 5 male      10 agree                0.454     0.0544   0.428     0.481 
 6 female    10 agree                0.472     0.0496   0.448     0.496 
 7 male      16 agree                0.475     0.0489   0.451     0.499 
 8 female    16 agree                0.461     0.0504   0.437     0.486 
 9 male      10 disagree             0.125     0.0937   0.106     0.147 
10 female    10 disagree             0.151     0.0834   0.132     0.174 
11 male      16 disagree             0.203     0.0756   0.180     0.228 
12 female    16 disagree             0.235     0.0721   0.210     0.261 
13 male      10 strongly.disagree    0.0491    0.120    0.0392    0.0613
14 female    10 strongly.disagree    0.0624    0.110    0.0509    0.0762
15 male      16 strongly.disagree    0.0935    0.101    0.0780    0.112 
16 female    16 strongly.disagree    0.117     0.0968   0.0990    0.138

ggeffects::ggemmeans(model = fit_polr_2,
                     terms = "female",
                     condition = c(educate = 12,
                                   polviewsN  = 4.5))

# A tibble: 8 x 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <fct>             <fct>
1 male      0.335    0.0169    0.302     0.368  strongly agree    1    
2 male      0.467    0.0124    0.442     0.491  agree             1    
3 male      0.141    0.00969   0.122     0.160  disagree          1    
4 male      0.0570   0.00571   0.0458    0.0682 strongly disagree 1    
5 female    0.281    0.0141    0.254     0.309  strongly agree    1    
6 female    0.477    0.0121    0.453     0.501  agree             1    
7 female    0.169    0.0101    0.149     0.189  disagree          1    
8 female    0.0723   0.00653   0.0595    0.0851 strongly disagree 1

13.6.1 Plot Predicted Probabilites

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>%  
  ggplot(aes(x = x,
             y = predicted,
             color = group,
             shape = group)) +
  geom_point(size = 4) +
  geom_line(aes(linetype = group)) +
  facet_wrap(~ response.level)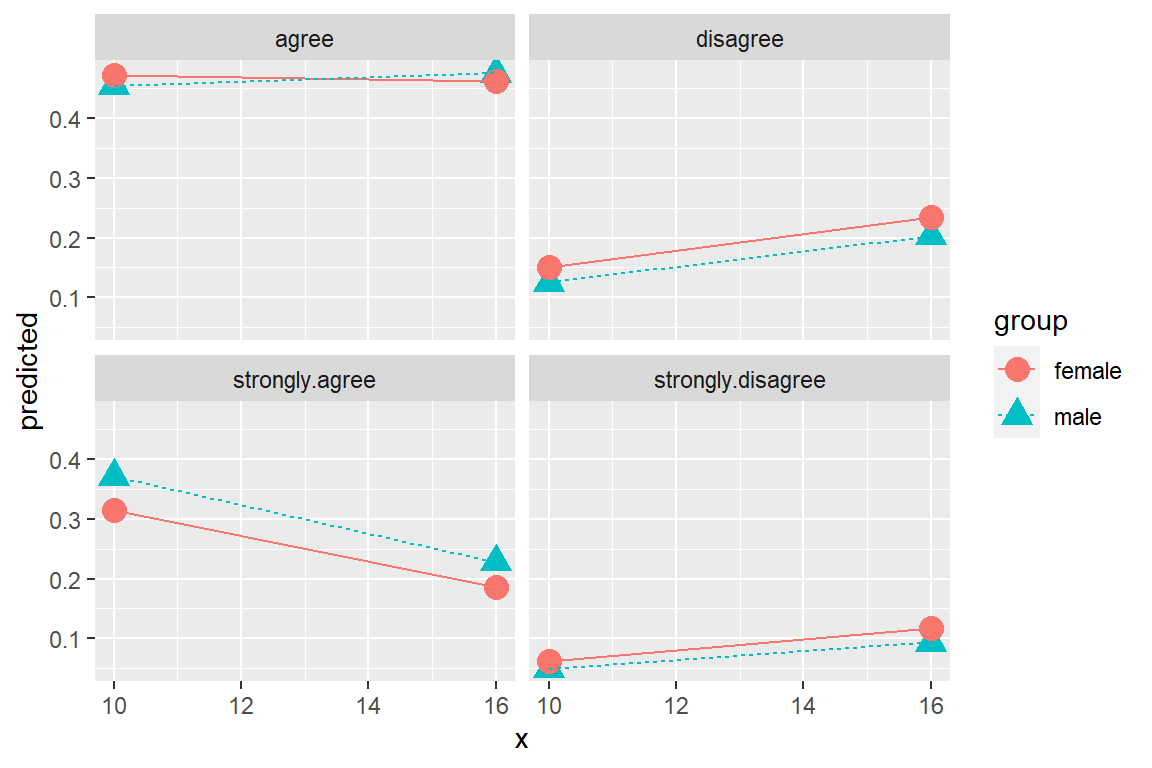

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level == "strongly.agree") %>% 
  ggplot(aes(x = x,
             y = predicted,
             color = group)) +
  geom_point(size = 4) +
  geom_line(aes(linetype = group))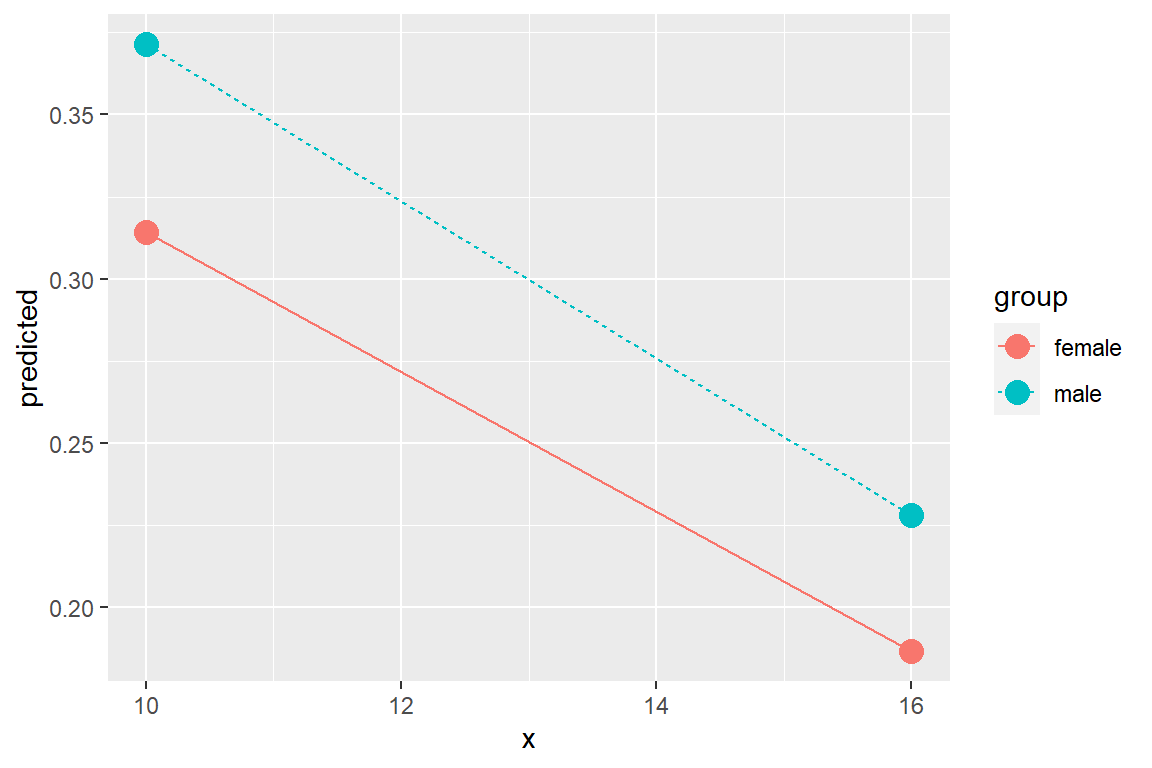

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level == "strongly.agree") %>% 
  ggplot(aes(x = x,
             y = predicted,
             color = group,
             shape = group)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .5,
                position = position_dodge(width =.25)) +
  geom_point(size = 4,
             position = position_dodge(width =.25)) +
  geom_line(aes(linetype = group),
            position = position_dodge(width =.25)) +
  theme_bw() +
  labs(x = "Education, years",
       y = "Predicted Probability for Strongly Agree",
       color = NULL,
       shape = NULL,
       linetype = NULL)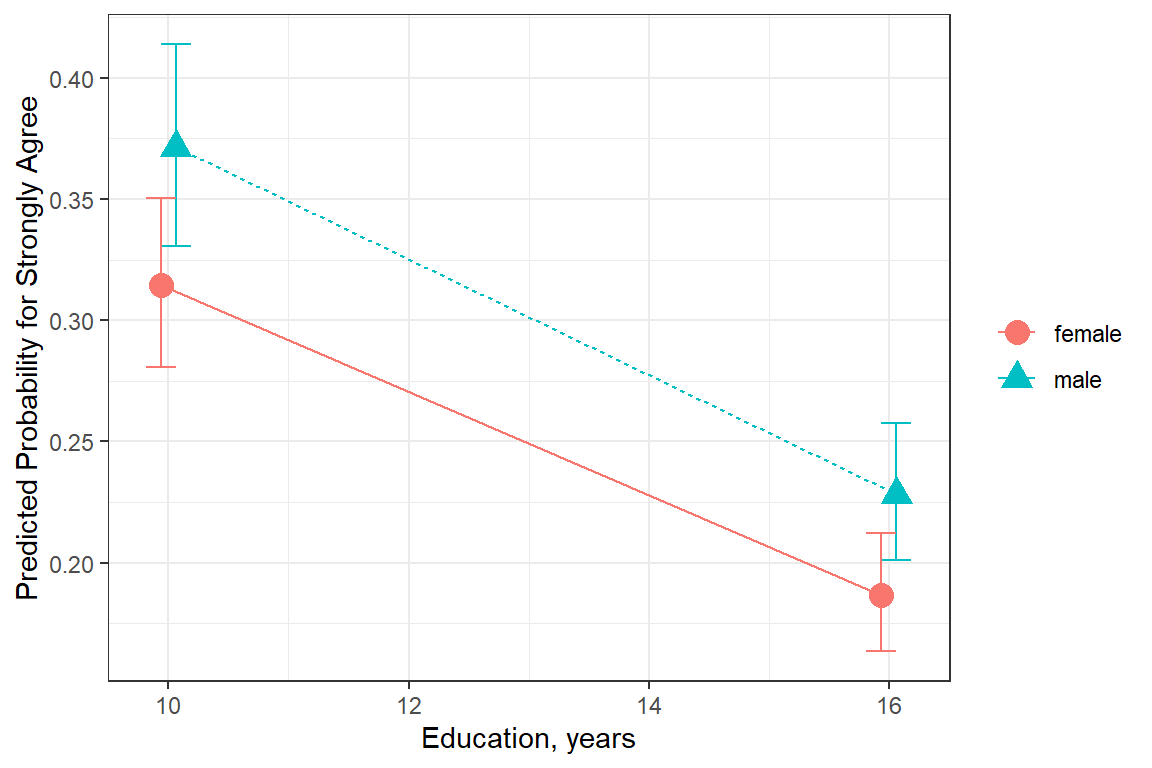

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::mutate(group = forcats::fct_rev(group)) %>% 
  dplyr::filter(response.level == "strongly.agree") %>% 
  ggplot(aes(x = x,
             y = predicted,
             shape = group)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .25,
                position = position_dodge(.2)) +
  geom_point(size = 4,
                position = position_dodge(.2)) +
  geom_line(aes(linetype = group),
            size = 1,
            position = position_dodge(.2)) +
  theme_bw() + 
  theme(legend.position = c(1, 1),
        legend.justification = c(1.1, 1.1),
        legend.key.width = unit(2, "cm"),
        legend.background = element_rect(color = "black")) +
  scale_linetype_manual(values = c("solid", "longdash")) +
  labs(x = "Years of Formal Education",
       y = "Predicted Probabilit for\nResponding 'Strongly Agree'",
       color = NULL,
       shape = NULL,
       linetype = NULL,
       title = "Adjusted Predictions: Strongly Agree Spanking is Appropriate")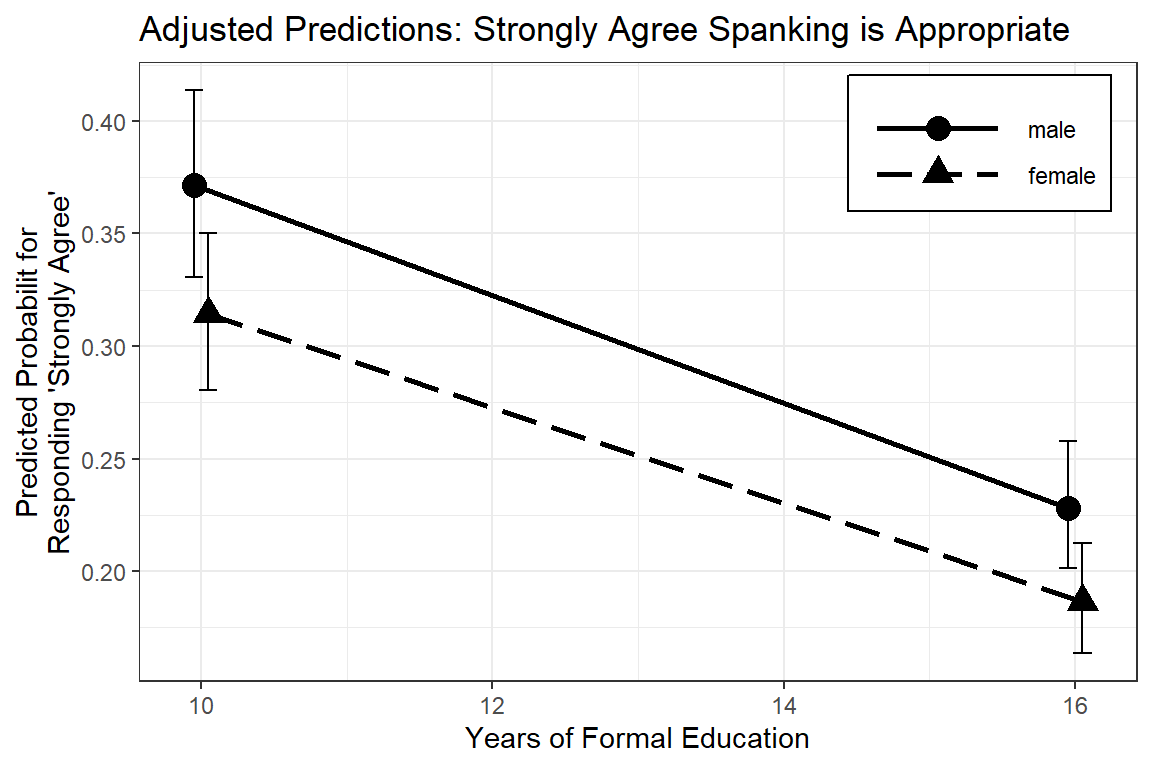

Figure 13.5: Hoffmann’s Figure 4.4

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level %in% c("strongly.agree",
                                      "strongly.disagree")) %>% 
  dplyr::mutate(resonse.level = factor(response.level)) %>% 
  ggplot(aes(x = x,
             y = predicted,
             fill = resonse.level)) +
  geom_col(position = position_dodge())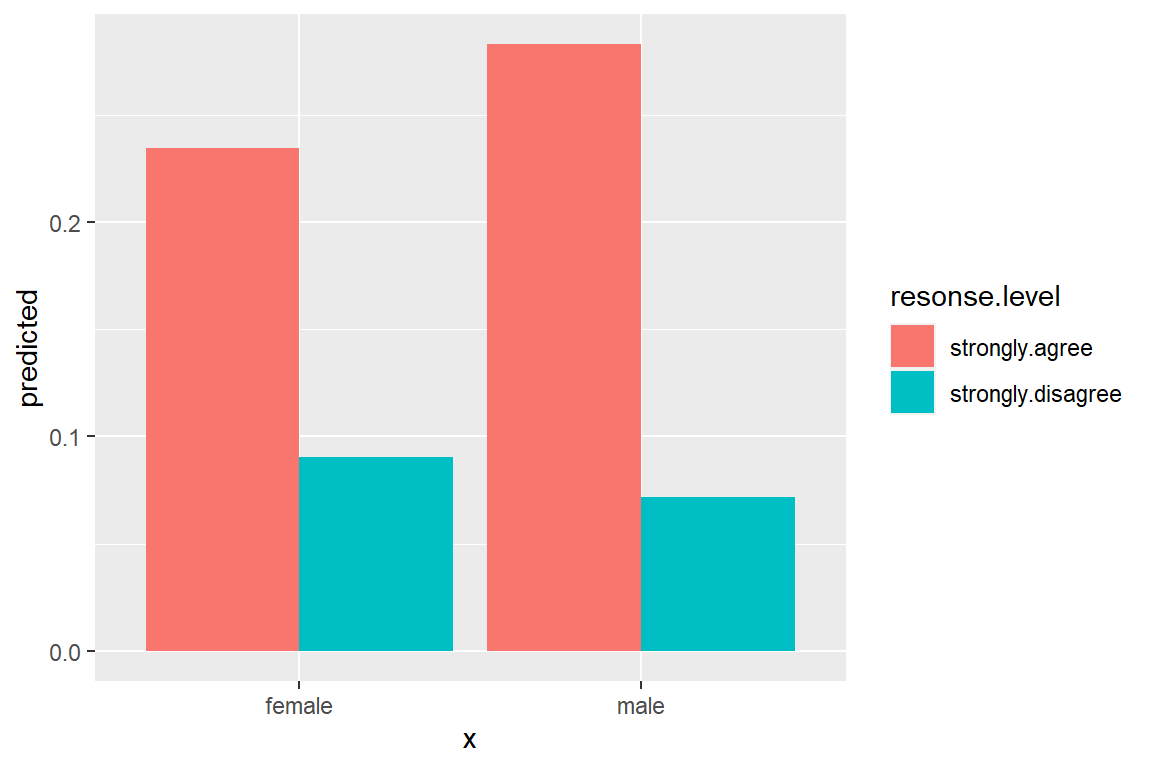

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level %in% c("strongly.agree",
                                      "strongly.disagree")) %>% 
  dplyr::mutate(resonse.level = factor(response.level)) %>% 
  ggplot(aes(x = forcats::fct_rev(x),
             y = predicted,
             fill = resonse.level)) +
  geom_col(position = position_dodge()) +
  theme_bw() +
  theme(legend.position = "bottom") +
  scale_fill_manual(values = c("gray30", "gray70")) +
  labs(x = NULL,
       y = "Predicted Probability of Response",
       fill = NULL,
       title = "Attitues towareds Spanking, by Sex")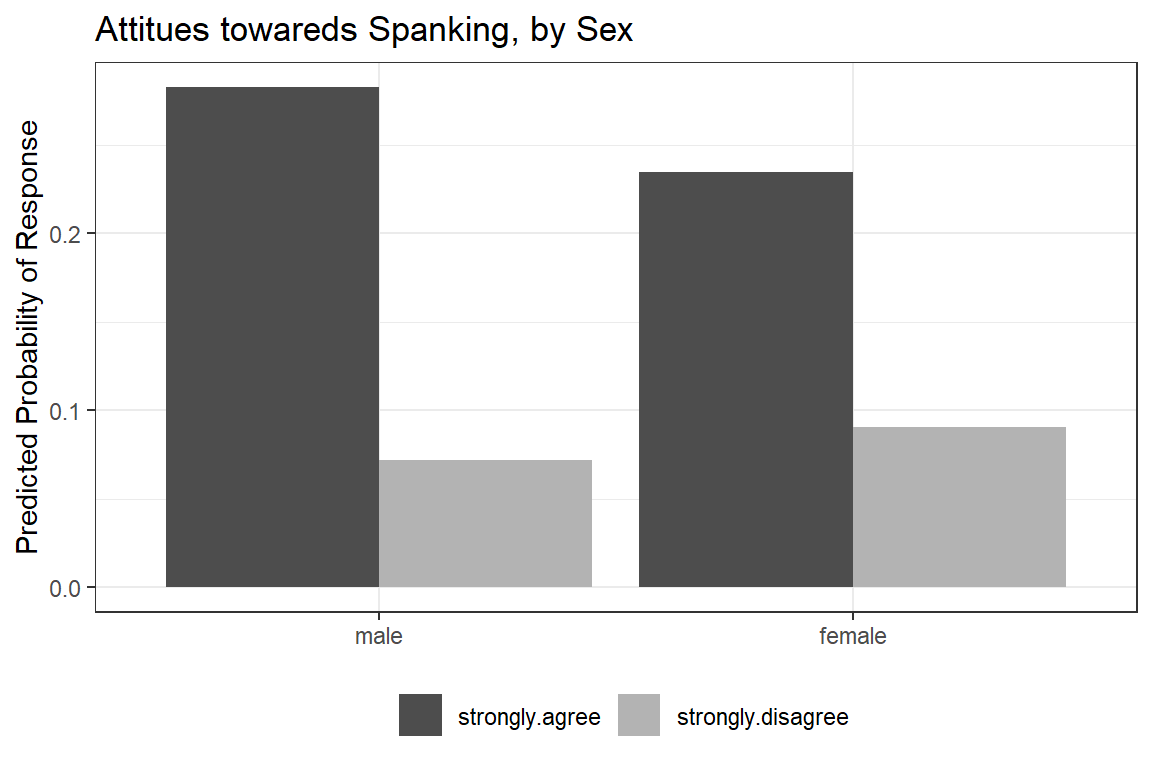

Figure 13.6: Hoffmann’s Figure 4.5

13.6.2 Model Fit and Variance Explained

fit_polr_1redeo <- MASS::polr(spanking ~ female,
                         data = data_gss_model %>% 
                           dplyr::filter(complete.cases(educate, polviewsN)))

anova(fit_polr_2, fit_polr_1redeo)

# A tibble: 2 x 7
  Model             `Resid. df` `Resid. Dev` Test   `   Df` `LR stat.` `Pr(Chi)`
  <chr>                   <dbl>        <dbl> <chr>    <dbl>      <dbl>     <dbl>
1 female                   1817        4501. ""          NA        NA         NA
2 female + educate~        1815        4397. "1 vs~       2       105.         0

performance::compare_performance(fit_polr_2, fit_polr_1redeo, rank = TRUE)

# A tibble: 2 x 8
  Name            Model   AIC   BIC R2_Nagelkerke  RMSE Sigma Performance_Score
  <chr>           <chr> <dbl> <dbl>         <dbl> <dbl> <dbl>             <dbl>
1 fit_polr_2      polr  4409. 4442.       0.179    2.06  1.56               0.8
2 fit_polr_1redeo polr  4509. 4531.       0.00384  2.06  1.57               0.2

13.6.3 Assumptions

13.6.3.1 Proportional Odds: Brant Test

The poTest function implements tests proposed by Brant (1990) for proportional odds for logistic models fit by the polr() function in the MASS package.

# Hoffmann's Example 4.8
car::poTest(fit_polr_2)


Tests for Proportional Odds
MASS::polr(formula = spanking ~ female + educate + polviewsN, 
    data = data_gss_model)

             b[polr] b[>strongly agree] b[>agree] b[>disagree] Chisquare df
Overall                                                             8.80  6
femalefemale  0.2532             0.2342    0.2180       0.4719      2.64  2
educate       0.1153             0.1248    0.1036       0.0927      1.17  2
polviewsN    -0.2215            -0.1622   -0.2558      -0.2872      4.85  2
             Pr(>Chisq)  
Overall           0.185  
femalefemale      0.268  
educate           0.558  
polviewsN         0.089 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A significant test statistics provides evidence that the parallel regression assumption has been violated!